This is a level 4 activity from the Figure It Out series.
A PDF of the student activity is included.
Click on the image to enlarge it. Click again to close. Download PDF (1137 KB)
Spatial-visualisation skills are important in many technical and scientific occupations. Reading, making, and using diagrams are good ways for students to develop these skills.
In these activities, students construct models and interpret two-dimensional representations of three-dimensional objects.
a classmate
FIO, Technology in Practice, Levels 3+-4+, Emergency Shelters, pages 14 - 15
sticky tape
thin card
scissors
Activity One
Question 1 is challenging. If necessary, scaffold the problem by asking the students these questions:
- How can you find the area of the board? (20 x 30 = 600 cm2)
- What will the area of each rectangle be? (600 cm2 ÷ 12 = 50 cm2)
- Can you draw some rectangles that have an area of 50 cm2?
Students could also divide a 20 cm x 30 cm piece of paper into 12 rectangles to find the dimensions. Note that the 2:1 ratio between length and width must be maintained. Be aware that an A4 sheet is very close to, but not equal to, 20 x 30 cm.
The hexayurt was designed by Vinay Gupta. See www.hexayurt.com for related links, including a video about how to make a folding hexayurt.
Examples of modified hexayurts are also available online and can be easily found by doing a search for “new hexayurts”. See www.tilings.org.uk/Hexayurt_Family.pdf to access Edmund Harriss’s nets of hexayurt relatives, “the tri-dome” and “the quad-dome”. Both these structures are based on the 2:1 rectangle and triangles.
Activity Two
This activity involves using different units of length (centimetres and metres). Give your students practice converting between the two units. They can choose whether to work in centimetres or metres, but remind them that when calculating perimeter or area, the measurements they use must have the same unit.
Students can find the number of tubes on each side by dividing the length of the wall by the diameter of each pole (360 ÷ 15 = 24). They may then make the mistake of simply multiplying this by 4 to find the total number of tubes. By doing so, each corner tube ends up being counted twice.
Multilink cubes can be used to show the relationship between the number of tubes on each side and the total number of tubes. For example: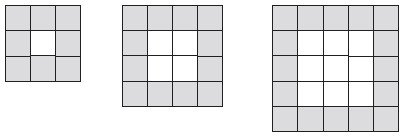
This can form the basis of a good investigation:
| Number of squares on each side | Total number of squares |
| 3 | 8 |
| 4 | 12 |
| 5 | 16 |
This will help students to identify that the total number of tubes is 4 times the number of tubes in each wall minus 4.
Interpreting a two-dimensional representation of a three-dimensional object requires good spatial-visualisation skills. Students who struggle to visualise the shapes that make up the roof may benefit from creating a model of it. This will help them to see that the roof is made up of two rectangles and two triangles.
Alternatively, students could construct a scale model of the entire shelter.
To estimate how many emergency shelters could fit on the school field, students could pace out the field to estimate its dimensions and then pace out the amount of space required for each shelter. Another option is to work out the dimensions of the field using an online map and then use a scale drawing or calculation to work out how many shelters would fit on it.
Working in a group to estimate the number of emergency shelters that could fit on the school field is a good opportunity to develop the key competency participating and contributing.
Technology-related student activities
- Construct models of emergency shelters using paper, card, and ice-block sticks. Investigate how well the models cope with wind produced by a fan or leaf blower.
- Research commercially made survival suits and the materials used to make them.
- Research other emergency shelter designs. For examples, see http://weburbanist.com/2008/11/12/ lifesaving-temporary-emergency-shelters-buildings
Exploring the technology-related context
Technological practice is often undertaken in an attempt to address a need. Floods and earthquakes often result in a loss of homes. Emergency shelters need to be easy to assemble, durable and, as far as possible, comfortable. The materials used to make them need to be readily available and affordable.
Answers
Activity One
1. a. 5 cm x 10 cm. The area of the card is 600 cm2 (20 x 30). Each hexayurt rectangle will have an area of 50 cm2 (600 ÷ 12). The rectangles are twice as long as they are wide, so the rectangles will be 5 cm x 10 cm. Another way to find the dimensions is to draw a diagram: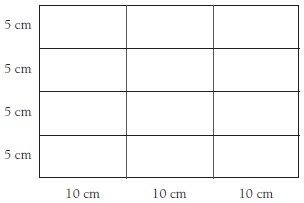 or
or 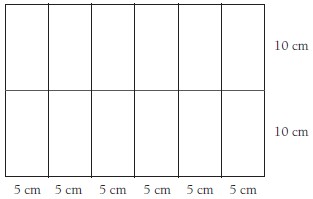
b. Not all rectangles that are 600 cm2 can be divided into exactly twelve 2:1 rectangles. For example, if the rectangle were 1 cm x 600 cm, it would be impossible to cut out even one 5 cm x 10 cm rectangle.
2. a. Practical activity.
b. Approximately 2 m. Answers will vary slightly, but a perfectly constructed hexayurt will have a height equal to the length of one of its walls.
3. No. The hexayurt design only works because the base of the roof triangle is the same length as the side of the rectangle. If the 2:1 ratio is changed, this relationship no longer exists.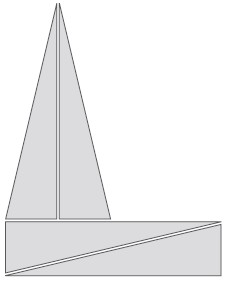
4. Practical activity. Designs will vary.
Activity Two
1. a. The base is 360 cm by 360 cm. 360 ÷15 = 24 tubes. Without taking into account the door and the window, there are 24 + 24 + 22 +22 = 92 tubes for the walls. The door takes up the space of 6 tubes (90 cm ÷ 15 = 6). The window takes up the space of 4.5 tubes (90 cm ÷ 15 = 6, and the window is 3/4 of a tube high, so altogether this is 4.5 tubes). Total number of tubes is 92 – 6 – 4.5 = 81.5 tubes.
b. The length of double-sided tape is the same as the total length of the tubes. 200 cm = 2 m. 2 m x 81.5 tubes = 163 m of double-sided tape.
c. The length needed for the frame is 360 x 6 + 200 x 6 = 3 360 cm (33.6 m).
d. Plastic sheeting (without allowing for overlap) is 17.64 m2: The roof is made from 2 rectangles and 2 triangles.
- area of 1 rectangle: 2 m x 3.6 m = 7.2 m2
- area of 1 triangle: 1/2 x 0.9 m x 3.6 m = 1.62 m2
Total area of 2 rectangles and 2 triangles is 7.2 m2 + 7.2 m2 + 1.62 m2 + 1.62 m2 = 17.64 m2
2. a.–c. Practical activity.

