This unit has a brief look at what is known about Egyptian Fractions. These are unit fractions – fractions whose numerator is one. We look at how fractions can be represented in terms of Egyptian Fractions. Finally we suggest a web site that students might like to use as resource material for a small project. Students also practice adding and subtracting fractions, and looking for patterns.
- Add and subtract fractions.
- Look for patterns and make conjectures.
- Consider infinity in a new situation.
In this unit we spend a great deal of time adding and subtracting fractions in the context of Egyptian Fractions. The outline of the unit looks more like an investigation of Egyptian Fractions than a series of lessons that reinforce arithmetic of fractions. So problem solving is applied to Egyptian Fractions to see what we can find out about them.
The questions that we explore here are of the type that mathematicians ask in their research. These are:
Can something be done? (Can fractions be represented in terms of Egyptian Fractions?)
Is something closed under an operation? (Is the sum of two Egyptian Fractions an Egyptian Fraction?)
If something is closed only sometimes, when does this happen? (When is the sum of two Egyptian Fractions an Egyptian Fraction?)
Can something be done in a particular way? (Can a fraction be represented as the sum of two Egyptian Fractions; three Egyptian Fractions; …?)
Is there an algorithm for finding something? (Is there an algorithm for finding a representation of a fraction as an Egyptian Fraction?)
Can something be done in an infinite number of ways? (Can a fraction be written as a sum of Egyptian Fractions in an infinite number of ways?)
As part of this unit we suggest that students undertake a project based on material that they can find on the Internet. This is scheduled for the last teaching session of the unit. In order for it to be completed then, it will probably be necessary for the students to begin work on it before that lesson.
Session 1
For some reason that is not clear, Ancient Egyptians only used fractions with a numerator of 1, with one exception (2/3). In this unit we want to explore that situation. In this first lesson we have a look at the sum of two Egyptian Fractions to see if we can get another Egyptian Fraction.
- Introduce the idea of Egyptian Fractions to the class. Ask them if they can think of any reason why the Egyptians were hooked on fractions with a one in the numerator. (Be sure to use the words numerator and denominator.) Accept any explanation no matter how fanciful as we do not know why they did.
- Have a look at some examples of Egyptian Fractions. Take 1/4 and 1/12.
What is the sum of these two fractions?
Work out the example with the help of the class.
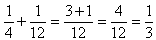
- Now the interesting thing about this is that the sum of two Egyptian Fractions is an Egyptian Fraction. Ask
Is this always the case?
Is the sum of two Egyptian Fractions always an Egyptian Fraction?
Take a vote and record the number in favour and those against it being true. Make a class conjecture. - Let them then go off in their groups to find evidence for or against the conjecture. In Copymaster 1 we have given a few Egyptian Fractions for the students to get started on. Get the groups to do the additions on that page to see what it tells them about the conjecture they have made. Then let them invent their own pairs of Egyptian Fractions and see if the sums of their Egyptian Fractions are Egyptian Fractions or not.
- Bring the class together and get them to discuss the conjecture. Is it true or is it false? What evidence do they have?
- On the board write down in one column those pairs of Egyptian Fraction that sum to a unit fraction and, in another column, write those that don’t.
Is there any pattern here?
Can you see anything in common between the Egyptian Fraction in the each column?
Are there any patterns that work for some of the pairs of Egyptian Fraction?
Let the groups work on these questions to see what they can find. If they are having difficulty you might want to give them some hints. - Now in the first five examples on Copymaster 1 we have definitely led the students in a particular direction. It turns out that (i) if the denominators of two Egyptian Fraction are n + 1 and n(n + 1), then the two Egyptian Fractions add to an Egyptian Fraction; and (ii) if the two denominators are da and db where a and b have no factors in common and a + b divides d, then the sum of the two Egyptian Fraction is an Egyptian Fraction. So there are patterns to be found.
- Students should soon discover for themselves that the sum of two Egyptian Fractions is not necessarily an Egyptian Fraction. This will settle the conjecture one way or the other (depending on which way they voted). It will take a little more effort to see the first of the patterns above, and even more effort to see the second one. So you may need to lead them to the second one. But that can come later.
- After some discussion you can say it looks like as if
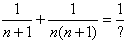
where the ? stands for something.
But what do you think it stands for?
And how would you find it?
Let them work this out in their groups. If some groups are unable to handle the algebra, then they should be encouraged to try some more examples (other than those on Copymaster 1) in order for them to see that this works for any value of n that they choose. Note that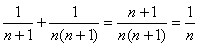 (a)
(a)
Pattern (ii) above is more complicated and could be reserved for the more able students. Here we get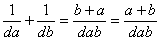
so if a + b divides d, then the fraction simplifies to give one in the numerator. Again, for weaker students the pattern can be reinforced by doing some particular examples.
- But there are patterns the other way. Did the class manage to find any patterns where two Egyptian Fractions did not add to an Egyptian Fraction? Certainly if the Egyptian Fractions have denominators that are primes (or have no factors in common), then their sum is not an Egyptian Fraction. Check what they have found here and lead them in this direction if necessary.
- Get the students to make a summary of what they have found in this lesson.
Session 2
In the last lesson we looked at when two Egyptian Fractions can be added together to give another Egyptian Fraction. Here we want to turn that idea around to see if an Egyptian Fraction can be written as the sum of two Egyptian Fractions. It turns out that this can always be done. But can an Egyptian Fraction be written as the sum of three, four, … Egyptian Fractions.
- Remind the class what an Egyptian Fraction is and that, in the last lesson, they were adding two Egyptian Fractions.
What sums did we get? - Can we turn this question around?
Can an Egyptian Fraction be written as the sum of two Egyptian Fractions?
Again you might like to let them guess what the answer will be. Get them to work in their groups on the Egyptian Fractions in Copymaster 2. If they think that they can see a pattern, get them to say what the pattern is and justify it. - The answer follows very quickly from equation (a) of lesson 1. Just make 1/n the subject. Then it can be seen that any Egyptian Fraction can be written as the sum of two Egyptian Fractions.
- There is one Egyptian Fraction that we haven’t given much thought to and that is 2/3.
Can 2/3 be written as the sum of two Egyptian Fractions? - Put equation (a) and the answer that the groups obtained for 2/3 on the board.
But if we can write any Egyptian Fraction as the sum of two Egyptian Fractions, can we write them as the sum of three Egyptian Fractions?
What about four Egyptian Fractions?
Can you find some examples of each?
Can you find a general pattern?
Let the class consider these questions in their groups. (They might like to use the Egyptian Fractions in Copymaster 2.) - Discuss the results that the students have found. Make sure that they can justify whatever claims they make – whether these be about specific cases, conjectures of what might be true or justifications/proofs. You should be able to lead them to see that any Egyptian Fraction can be written as the sum of any number of Egyptian Fractions simply by using equation (a) a sufficient number of times. For instance, suppose that we wanted to write 1/3 as the sum of three Egyptian Fractions. Then we could tackle it this way:
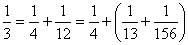
To make 1/3 the sum of four Egyptian Fractions we simply use equation (a) again to expand 1/156.
- Give students time to write down what they have found during the course of this lesson.
Session 3
We now have a pretty good idea of what we can do just using Egyptian Fractions. However, there are lots of fractions that are not Egyptian Fractions. So in this lesson, we consider how to split up arbitrary fractions into Egyptian Fractions.
- Remind the class that we have been looking at Egyptian Fractions and that in the last lesson we found that.
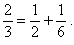
Can every fraction be expressed as the sum of two or more Egyptian Fractions?
What do you think?
Note that we can’t use the same Egyptian Fraction more than once. If we could, then we could have written 2/3 as simply two 1/3s.
Take a vote and formulate a conjecture as a result. This conjecture may say yes they all can or no, there are some that can’t. Let the students go into their groups to consider the fractions, 1/5, 2/5, 3/5 and 4/5.
- Get them to report back to the class. Summarise the results on the board.
What do these results tell us about our conjecture?
All of the fractions we have considered do have Egyptian Fraction representations.
How did you go about finding these representations?
Did you guess and check or did you have a system?
See if they have found any systematic way to produce their representations. - A method of finding the Egyptian Fraction representation of 4/5 might be helpful. Now 4/5 = 0.8.
What Egyptian Fraction is smaller than 0.8 but closest to it? (1/2)
So start with 1/2 as the first Egyptian Fraction. Now subtract 1/2 from 4/5 to see if we have an Egyptian Fraction or not. The answer is 3/10. This is 0.3.
What Egyptian Fraction is smaller than 0.3 but closest to it? (1/4)
So start with 1/4 as the first Egyptian Fraction fro 3/10. Now subtract 1/4 from 3/10 to see if we have an Egyptian Fraction or not. The answer is 1/20.
This means that our Egyptian Fraction representation for 4/5 is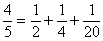
- There are two things to notice now. First, we have a method of at least looking for an Egyptian Fraction representation of any fraction. Second, we have found our first fraction that seems to need more than two Egyptian Fractions. Hold onto this latter idea for a moment and give the students a chance to practice the method that we have shown above.
Using the method we have just looked at, can you find the Egyptian Fraction representation for the following fractions: 5/6, 4/7, 3/7, 6/7 and 59/140?
Give them time to work on these in their groups.
(In this exercise there is the opportunity for some useful teaching on the comparison of fractions. As you see, we have done this via decimals. What we have done is not easy and students may find it takes time to come to grips with the process.) - Give the students time to summarise what they have done during this lesson. This may mean that you will have to carry over the completion of the last exercise until the next lesson.
Session 4
In this session we look at how else we could apply the method of finding an Egyptian Fraction representation. This will show us that there is more than one way of finding an Egyptian Fraction representation for a given fraction.
- Remind the class of the method they used in the last lesson to find Egyptian Fraction representations for a given fraction. Go through the representation of 59/140 with the class as a whole.
- Then recall the Egyptian Fraction representation for 4/5. Here we started with ½ because it was the largest Egyptian Fraction less than 4/5.
What if we chose to start with 1/3 instead?
Can we get an Egyptian Fraction representation this way too?
Give them time to work this out. (The quicker students could be asked to try starting with ¼.) - It seems that we can get an Egyptian Fraction representation starting with any Egyptian Fraction that is less than our target fraction.
See how many Egyptian Fraction representations you can find for 5/6, 3/7 and 4/7? - Your students should be able to get infinitely many representations for each of these as there are an infinite number of places to start. (You can just take smaller and smaller and smaller Egyptian Fractions as your starting point.) Discuss this with the class and help them to realise that there is no end to the number of representations they can find.
- Now the method they have been using is called an algorithm. This is a mechanical way that must produce an answer. Here the method that uses the largest Egyptian Fraction less than the fraction at each stage will terminate. In other words it will eventually stop on a fraction with a numerator of one. So that method will eventually produce an Egyptian Fraction representation for any fraction.
But choosing an arbitrary Egyptian Fraction at each stage will also eventually terminate and so will produce an algorithm too.
- In discussion with the students summarise what has been found in the four lessons so far. Get them to write this up. The summary might include:
- what is an Egyptian Fraction;
- every Egyptian Fraction can be written as the sum of two other Egyptian Fractions;
- every fraction can be written as the sum of different Egyptian Fractions;
- there is an algorithm that will find the Egyptian Fraction representation of any fraction;
- what is an algorithm;
- every fraction can be written as the sum of different Egyptian Fractions in an infinite number of ways.
Session 5
There is still a considerable amount to learn about Egyptian Fractions. In this final lesson we ask student so produce a short report on an aspect of Egyptian Fractions. Students will be able to find a number of sites. The Egyptian Fractions Wikipedia page would be a good place to start.
- Ask students (either on their own, in pairs, or as a group) to produce a short report on an aspect of Egyptian Fractions.
- There are a number of things that they could report on. We suggest a few things here but you might have other things that they could consider or they could suggest their own topic.
- Why did the Egyptians use only ‘unit’ fractions?
- Why does the algorithm we used work?
- Which fractions can be represented by two Egyptian Fractions?
- Which fractions can be represented by three Egyptian Fractions?
- How did Egyptians calculate with their fractions?
- How can Egyptian Fractions be applied to other areas of mathematics?
- Perhaps you could put these reports into an Egyptian Fraction book. You might also allow each group to report on what they have found.