This is a level 3 algebra strand activity from the Figure It Out series.
A PDF of the student activity is included.
Click on the image to enlarge it. Click again to close. Download PDF (387 KB)
find a rule to describe a relationship
counters or multilink cubes
Before trying this activity, make sure that students read the questions carefully and note down important facts or restrictions.
- three bottles at a time
- always has one bottle with him except on last trip back
- no bottle on last trip
- ends back at the bore
- count one-way walks.
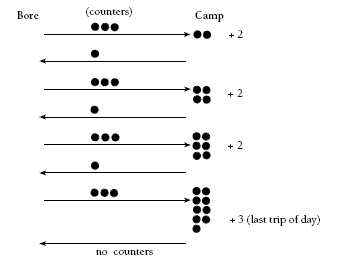
Students could model Duncan’s walks, using counters, pen, and paper.
For example:
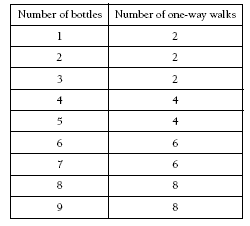
Using a table will help students identify patterns and suggest a rule:
Students could work in pairs or groups to suggest rules and then test them by modelling. Some examples could be:
- Answers must be even.
- Even numbers of bottles have the same value as the number of one-way walks taken to deliver them to the mining camp.
- Odd numbers of bottles would have a value one less than the number of trips taken.
The rule in question 3 is a complicated one for students to recognise. Duncan now takes four bottles per trip, three of which can be left at the mining camp unless it is the last trip of the day.
Ways in which students write their answers will vary, but they should notice that apart from thefirst group of four, the numbers of trips required for the numbers of bottles are in groups of three (compared to an initial three and then groups of two for the previous rule). That is, the same number of trips is required for one, two, three, or four bottles, and likewise for five, six, or seven bottles, and for eight, nine, or 10 bottles. This occurs because three bottles are left after each trip to the mining camp except for the last trip, when four can be left. Students might suggest this set of
rules:
- Take one off the number of bottles needed (Duncan can leave the extra one on his last trip).
- Round this number up to the next multiple of three (because three can be left each trip).
- Divide the number by three (because three bottles are left each time).
- Multiply by two (because Duncan has to go there and back).
Another set of rules is given in the answers.
Encourage students to explain their line of reasoning logically, either orally or in written form.
Answers to Activity
1. These answers include Duncan’s final walk back
to the bore.
8 bottles: 8 one-way walks
9 bottles: 8 one-way walks
7 bottles: 6 one-way walks
2. Answers will vary. Duncan delivers 2 bottles for every 2 one-way walks except on his last trip of the day, when he delivers up to 3 bottles. A rule could be: For odd numbers of bottles, take 1 off the number of bottles to find the number of oneway
walks. For even numbers of bottles, the number of bottles gives the number of one-way walks.
3. Answers will vary. Duncan delivers 3 bottles for every 2 one-way walks except on his last trip of the day, when he delivers up to 4 bottles. A rule could be: The number of one-way walks goes up in steps of 2, for example, 2, 3, and 4 bottles: 2
one-way walks; 5, 6, or 7 bottles: 4 one-way walks. Each group of 3 has a multiple of 3 in the centre. Finding 2/3 of the number of bottles for these multiples of 3 gives the number of one-way walks, for example, 2/3 of 6 is 4 one-way walks.