Purpose
The purpose of this activity is to support students in using doubling and halving to find the factors of a given number.
Achievement Objectives
NA2-1: Use simple additive strategies with whole numbers and fractions.
Required Resource Materials
- Square tiles or squared paper
- Calculators
Activity
- Engage students in a discussion about quilt or tapa cloth making. This might involve talking with local community members or looking at real (or pictures of) quilts or tapa cloth. Discuss how quilts and tapa cloth are made and highlight that the pattern blocks are often squares joined in a tessellation. Te reo Māori kupu such as whakarea (times, of, multiply) and tūtohi tukutuku (array) could be used throughout this activity.
- Imagine that you have 24 squares to make a quilt or tapa cloth. The finished quilt/cloth must be a rectangle. How big might the quilt/cloth be?
Let students experiment with 24 square tiles, grid paper, or a digital representation of squares, to find a possible rectangle with a total area of 24 squares. After an appropriate time gather the group to discuss possible answers. Possibilities include: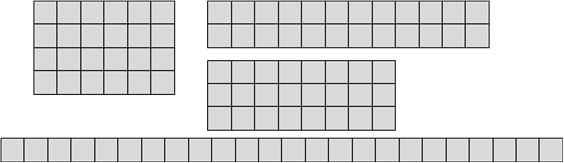
- Gather together and discuss the size of students' designs.
How can we write the size of each quilt/tapa cloth?
Can we use multiplication?
The size of designs shown above could be recorded as 1 x 24, 2 x 12, 3 x 8, and 4 x 6.
Do you think we have found all the possible sizes? How do you know?
Students may not regard 1 x 24 and 2 x 12 as viable quilts/ tapa cloths.
- Now that we have found some answers I wonder if there was an easy way to find them. Provide time for students to discuss this idea with a partner.
1 x 24 is easy to find. What other sizes would be easy to find? Is there a pattern that starts with 2 x ? Encourage students to systematically think about a pattern using the given array sizes (e.g. 1 x 24, 2 x 12, 4 x 6).
What pattern do you notice?
Students might notice that doubling one number in the expression, and halving the other, gives another suitable array size.
You might show the two arrays that match the facts so students can compare them visually.
What would happen if we doubled and halved again? (4 x 6)
What would happen if we doubled and halves with 4 x 6? (8 x 3)
- You may have noticed that a 24-square quilt/tapa cloth is a bit small. Let’s double the number of squares to make it bigger.
What is double 24?
Agree that double 24 equals 48 squares.
Before you start finding the sizes of the quilt/tapa cloths think about what you learned from the 24 square quilt. You can use the calculator if that helps.
- Let students attempt to find all the possible 48-square quilts/tapa cloths using tiles, grid paper, and calculator. Allow them to work in appropriate groupings that will encourage scaffolding, extension, and productive learning conversations, and to express their mathematical ideas in a range of ways (e.g. as diagrams, written equations, verbally). Roam as students work and look for them to do the following:
- Represent the possible sizes as multiplication
- Use the sizes for 24 squares to pre-empt what will work for 48 squares
- Start with 1 x 48 and use doubling and halving
- Use their known multiplication facts (e.g. 4 x facts) to investigate possible sizes.
- Gather the group after a suitable time. Discuss how to find all the possible sizes for the quilt/tapa cloth.
Remember that we found 1 x 24, 2 x 12, 4 x 6, and 8 x 3 for the 24 square quilt.
Did anyone use those facts to look for sizes with 48 squares?
Did anyone use doubling and halving?
Record the sizes, as multiplication, as students offer them. Record the facts systematically to enhance the chance of pattern spotting:
1 x 48
2 x 24
4 x 12
8 x 6
16 x 3
Have we found them all? How do you know? Can you see a pattern?
Can we make a 5 x size quilt/tapa with 48 squares?
Next steps
- Explore other quilt/tapa cloth sizes with numbers of squares that have many factors, such as 36 squares and 60 squares.
- Progress from using materials to anticipating sizes using multiplication facts.
- Explore the division operation on the calculator to check for possible factors, such as dividing 48 by different numbers to see what factor occurs, e.g. 48 ÷ 3 = 16.
- Investigate the commutative property. Do 6 x 8 and 8 x 6 represent different quilts/tapa cloths or the same one?
Add to plan
Level Two