This problem solving activity has a statistics focus.
Dominoes are rectangles that have two lots of numbers on them.
The numbers range from 0 to 6 and are usually indicated by dots in the same way that a dice is numbered.
How many different dominoes are there in a set?
- Apply counting strategies to problem solving tasks.
- Write an explanation of what they have done.
- Devise and use problem solving strategies to explore situations mathematically (constructing a tree diagram, be systematic, make a list).
This problem explores tree diagrams and other counting methods, including making an organised list. Both strategies help students to show that they have considered all possible combinations and that none is missed.
This part of mathematics is known as combinatorics. Counting techniques can become sophisticated quite rapidly.
- Copymaster of the problem (Māori)
- Dominoes to introduce the problem
- Copymaster of the problem (English)
The Problem
Dominoes are rectangles that have two lots of numbers on them. The numbers range from 0 to 6 and are usually indicated by dots in the same way that a dice is numbered.
How many different dominoes are there in a set?
Teaching Sequence
- Show some dominoes and ask:
Have you played a game with dominoes?
How was it played? - Suppose we wanted to know how many are in a set if we didn't have one available to count.
How could we do it?
Could we solve a simpler problem first?
How might we do this? Suggest and discuss the different approaches that can be used to count the 0-2 dominoes. For example:
Organised list
0, 0
0, 1
0, 2
1, 1 (note that 0, 1 is not listed as it is not distinguishable from 1, 0 in dominoes)
1, 2
2, 2Tree diagram
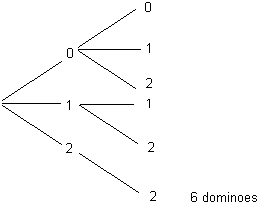
- Have the students work in pairs or small groups to solve the bigger problem or maybe even a smaller problem first (e.g. if the most spots on a domino is 4).
- Check the progress of each group. Give assistance where needed. Any group that finishes early can try the extension problem.
- Have the students report back to the whole class.
- Give them time to write up their method of solution.
Extension
If a set of dominoes had every number from 0 to 100, how many would there be in the set?
Can you extend this to every number between 0 and n?
Solution
Method 1: One way to look at this problem is to write out the possible outcomes. In other words, make an organised list. This is rather tedious but should give the right answer provided care is taken to include all dominoes.
Method 2: To help make this list-making process more systematic, use a tree diagram.
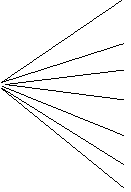
The first step takes the numbers 0 to 6 and gives the 7 branches of the tree above. Taking the 0 branch we can add 7 more branches, one for each number 0 to 7.
Now go to the 1 branch. Because we can’t tell the difference between the 0, 1 and the 1, 0 dominoes, we only need to add 6 branches here. This is one branch for each of the 1 to 6 set of spots. This gives 6 new branches.
Now go to the 2 branch. Here we only need to add branches for the numbers 2 to 6. There are 5 of these.
The 3 branch now contributes another 4 branches; the 4 branch a further 3; the 5 branch 2; and the 6 branch 1.
Hence we have a total of 7 + 6 + 5 + 4 + 3 + 2 + 1 = 28 end nodes. So there are 28 dominoes. Note that 28 is a triangular number. We often encounter these.
Method 3: Another way to do this is to say that we have a choice of 7 numbers for one end of the domino and 7 for the other end. This gives 49 but we haven’t finished yet. first of all note that there are 7 dominoes that have the same number at each end. So take these away from the 49 we have so far counted. The remaining ones (42 of them) occur in pairs like 2, 5 and 5, 2. We can’t tell these apart. So there are actually 42¸ 2 x 21 of these dominoes with different numbers at either end. Altogether then there are 21 + 7 = 28 dominoes.
Solution to the Extension
There are n + 1 choices for one end of the domino and n + 1 choices for the other end. So there look to be (n + 1)2 altogether. But take away the ones that have the same number of spots at either end. This removes n + 1 dominoes. So we now have (n + 1)2 – (n + 1) = (n + 1)n. These remaining dominoes occur in pairs. That means that we have n(n + 1)/2 of them.
The total number is then (n + 1) + n(n + 1)/2 = (n + 1)(n + 2)/2.
Check that this gives 28 when n = 6.
