This is a level 5 algebra strand activity from the Figure It Out series.
A PDF of the student activity is included.
Click on the image to enlarge it. Click again to close. Download PDF (124 KB)
usea table to continue a pattern
use a rule to describe a prediction
write a rule as a quadratic equation
FIO, Level 4+, Algebra, Book Four, Domino Stacks, page 14
dominoes (optional)
In this activity, students use number patterns to first devise a rule for the number of dominoes used in the bottom storey of any domino-stack house. They also devise a rule for the total number of dominoes in any domino-stack house.
In question 1, some students may find it helpful to use dominoes to build houses with 1 storey, then 2, 3, and 4 storeys. Others may find it sufficient to draw diagrams of such a sequence of houses.
The number of dominoes required forms a sequence of odd numbers, so we would expect the bottom storey of a 4-storey house to require 9 dominoes. This is correct, and the following diagram shows how it can be visualised:
There are 2 x 4 + 1 = 9 dominoes in the bottom storey of this 4-storey domino house. A house with n storeys will have 2 x n + 1 = 2n + 1 dominoes. (It is helpful to remember that 2n + 1 can be used to generate the odd numbers, 1, 3, 5, 7, … by finding its value when n = 0, 1, 2, 3, … respectively.)
Question 1d requires the students to work backwards and calculate how many storeys high a stack with 69 dominoes in its bottom storey would be. The students might choose to construct a flow chart or to approach the question algebraically: “We know that 2n + 1 = 69, so 2n = 68 and n = 34.”
In question 2, Barbara and Kahu make a table to help figure out a way to predict the total number of dominoes needed for any domino house. A rule for n storeys is: n x (n + 2), which simplifies to n(n + 2). There are other rules that some students may suggest, for example, n2 + 2n. Note that n(n + 2) = n2 + 2n, so these two rules are equivalent.
Using n2 + 2n for a domino house with 13 storeys, we find that it needs 132 + 2 x 13 = 13 x 13 + 26
= 169 + 26
= 195 dominoes.
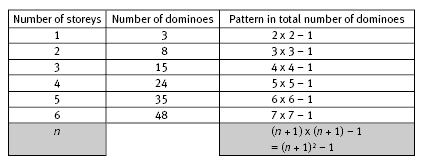
Students may also notice that the numbers, 3, 8, 15, 24, 35, … are all 1 less than the square numbers 4, 9, 16, 25, … respectively. The pattern related to this is shown in the following table:
So, for example, the number of dominoes for a domino house with 20 storeys is 21 x 21 – 1 = 440. It can also be shown that (n + 1)2 – 1 is equivalent to the rules n(n + 2) and n2 + 2n.
Question 2d i is easily solved using the n x (n + 1) rule. For question 2d ii, the students are looking for the greatest pair of numbers that are separated by 2 and that multiply to give no more than 4 899. The smaller of the two numbers is n, the number of storeys in the house.
The best approach for this question is a trial-and-improvement strategy, starting with a number that is less than the 76 used in 2d i. Some students may notice that 4 899 is 1 less than 4 900, which is 702. This suggests that the pair of numbers should be very close to 70. In fact, they are 69 and 71, which multiply together to give exactly 4 899, the maximum number of available dominoes. So the number of storeys is 69.
Answers to Activity
1. a. 9 dominoes
b. A possible rule is: the number of dominoes in the bottom storey = 2 x number of storeys + 1
c. 41 dominoes. (2 x 20 + 1)
d. 34 storeys. ((69 – 1) ÷ 2)
b. 120 dominoes
c. i. Answers may vary. One possible rule is: the total number of dominoes equals the number of storeys multiplied by 2 more than the number of storeys.
ii. The following rule is based on the rule above: for n storeys, there will be n x (n + 2) dominoes.
ii. 69 storeys. (A trial-and-improvement strategy is needed here.)