These are level 3 measurement and algebra problems from the Figure It Out series.
A PDF of the student activity is included.
Click on the image to enlarge it. Click again to close. Download PDF (383 KB)
solve problems involving lengths (Problem 1)
solve problems involving patterns and addition (Problem 4)
Problem One
Note that there will be small errors depending on the way that the coins are measured. The measurements given here are as accurate as possible.
a. There are 20 5-cent coins in $1, so there are 20 x 25 = 500 5-cent coins in $25.
A 5 cent coin has a diameter of about 1.9 centimetres. So the trail was 500 x 1.9 = 950 centimetres or 9.5 metres long.
b. There are 10 10-cent coins in $1, so there are 10 x 25 = 250 10-cent coins in $25. A 10 cent coin has a diameter of about 2.3 centimetres.
So the trail was 250 x 2.3 = 575 centimetres or 5.75 metres long.
Problem Two
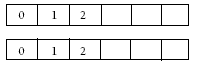
The students need to work systematically to arrange the digits on the cubes. For example:
• There are six faces on each cube.
• Which digits do they need two of? They need two of 1 and two of 2 to get 11 and 22. They also need a 0 to go in front of all the other nine digits (1–9), and because the nine digits won’t fit on one cube, they’ll need a 0 for both cubes. So far, this makes:
• 6 can go upside down as a 9.
• There are six digits left to be placed: 3, 4, 5, 6, 7, and 8. There are six places left on the cubes. It doesn’t matter which cube each digit goes on although, as noted in the Answers, there is only one solution if the cubes are based on the ones in the first illustration in the students’ book.
Problem Three
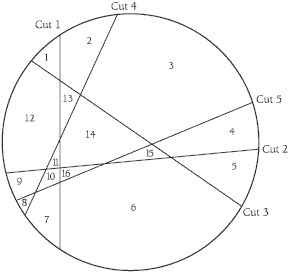
This problem is similar to Problem Four, page 1, but this time it is dealing with cuts in two dimensions rather than the three dimensions of the cheese problem. The same principle applies, though, that with every cut that the students make, they should try to divide as many existing pieces as possible. They should keep in mind that the pieces can be any shape or size.
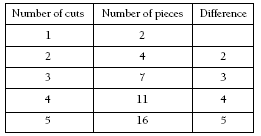
After a bit of experimenting, the students should be able to get 16 pieces. But is this the largest number of pieces with five straight cuts? The pattern below suggests that it is:
The pattern above also indicates that 22 cuts are possible with six straight cuts. In reality, some pieces may be so small as to be insignificant!
Problem Four, page 14, in Problem Solving, Figure It Out, Levels 2–3 and the corresponding teachers’ notes could be a useful warm-up for students who are having difficulty with this problem.
Problem Four
This is not a difficult problem, but the students will have to work systematically through the information to find the answer. Firstly, they need to work out how many tables are needed for each size group. Groups of one, two, three, or four will need one table each. Groups of five or six will need two tables each. (The illustration in the students’ book shows how six people sit around two tables.) Groups of seven or eight will need three tables.
Hints for Students
1. How wide is a 5 cent coin?
If you put the two 5 cent coins side by side, how wide is that? What about ten 5 cent coins? How many 5 cent coins in $25?
2. Look carefully at the 9 in the picture. What would happen if you turned it upside
down? Work systematically to put the digits on the cubes.
You could try a smaller case first.
3. To get the largest number of pieces, what do you want to do each time you make a cut?
4. How many tables will each group need? Work systematically.
Answers to Problems
1. a. 9.5 m (9 500 mm)
b. 5.75 m (5 750 mm)
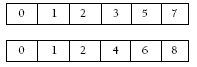
2. A possible answer (based on the cubes in the first illustration in the students’ book) is:
One cube: 0, 1, 2, 3, 4, and 6. (The 6 is used upside down as a 9.)
Other cube: 0, 1, 2, 5, 7, and 8.
On two blank cubes, each cube would have 0, 1, and 2. The 3, 4, 5, 6, 7, and 8 could go on either cube.
3. 16
4. 20