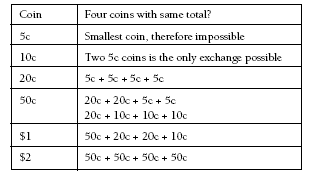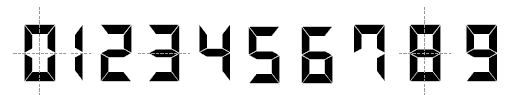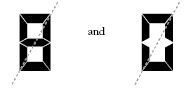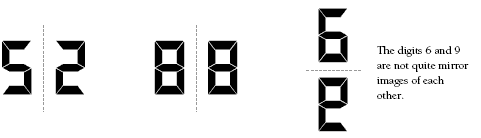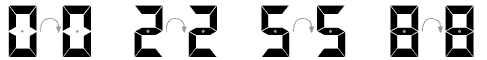Digit Detail

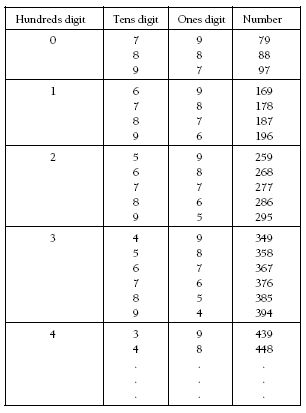
Problem One

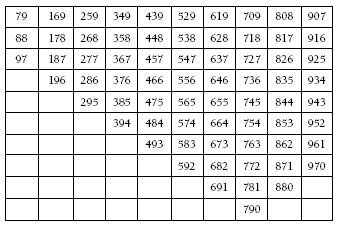
Encourage students to look for a systematic strategy to find all the possible solutions. They could use an organised list, a tree diagram, or a table. Here is how a table might be used to find all the possible solutions.

If students find this problem difficult, start with a digit problem that has fewer solutions, such as: “The digits of 57 add to 12. What other two-digit numbers have a digit sum of 12?”
“What three-digit house numbers have a digit sum of 21?”
Using digit cards may be helpful for some students as they try various possibilities.

Problem Two

Students might use a strategy of trying all the denominations of coins available and eliminating those that don’t work.

Only 20 cents and $2 can be made with four identical coins. However, 50 cents can be made with four coins in two ways and $1 can be made in one way.

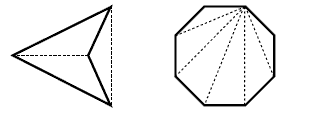
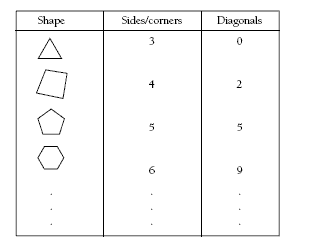
Problem Three

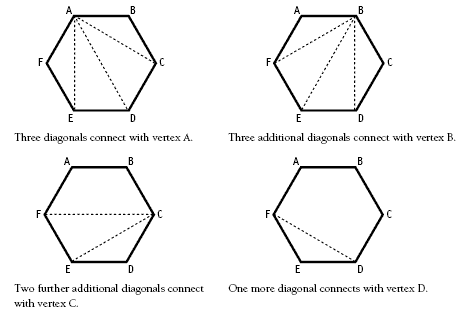
Students will need to understand that a diagonal connects a corner (vertex) of a polygon with any corner that is not adjacent to it. For example, these are diagonals:

Students need to approach the problem systematically and organise the results in a table or list. This will help them to identify patterns.

The table will show that the number of diagonals increases markedly with each side added, so the sides/corners and diagonals will not be equal for any other polygon.
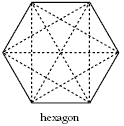
Students may be interested in looking at ways to work out the number of diagonals for a given polygon. Consider a hexagon:

So a hexagon has 3 + 3 + 2 + 1 = 9 diagonals.
This thinking can be used to show that a heptagon (seven-sided polygon) has 4 + 4 + 3 + 2 + 1 = 14 diagonals.

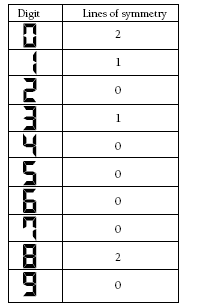
Problem Four

The digits shown in this problem are slightly different from those shown on some calculators. Some displays show the figures on a slight slant.
Some students may need a mirror to find the lines of symmetry by looking for mirror positions where part of the digit is masked yet the digit appears whole, as in the diagram below.
Vertical and horizontal lines are the easiest to find.

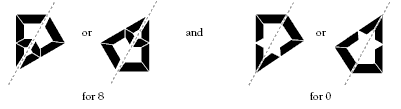
Some students may be confused by diagonal lines of symmetry. For example:

and are not lines of symmetry because when viewed in a mirror (depending on which way the mirror faces), the digits appear as:

When students put the mirror beside the digits, they will see that some digits are mirror images of other digits while others are their own image.

A similar analysis can be made of the rotational symmetry (turn symmetry) of each digit.

Each of the digits 0, 2, 5, and 8 has half-turn symmetry.

Problem Five

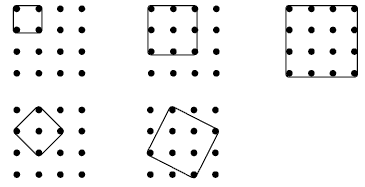
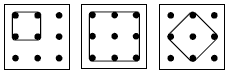
Diagonal squares are often overlooked by students. With a 3 x 3 geoboard, the possible squares are:

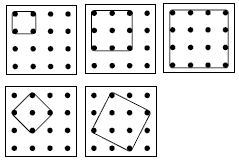
Moving to a 4 x 4 geoboard increases the number of possible squares. Students will need to adopt a systematic strategy, such as finding all the squares involving a corner pin and then finding all the squares involving a centre-side pin.

Answers to Problems

1.

2. $2 (4 x 50c) or 20c (4 x 5c) if the coins are identical; 50c (20c + 20c + 5c + 5c or 20c + 10c + 10c + 10c) or $1 (50c + 20c + 20c + 10c) if the coins are not identical
3. No. A triangle has no diagonals and a square has only 2 diagonals. Any polygon with more than 5 sides has many more diagonals than sides or vertices (corners). For example:

4. a.

b.

c.

5. a. 3

b. 5