This is a level 3 algebra strand link activity from the Figure It Out series.
A PDF of the student activity is included.
Click on the image to enlarge it. Click again to close. Download PDF (326 KB)
find and use rules in number patterns
FIO, Link, Algebra, Book One, Digit Chains, page 16
Most of the early difficulty that students have with digit chains arises from not understanding the given rule to make the numbers in the digit chain. It may be that their difficulties are related to confusion with the notion of digit as distinct from number. It is likely that some discussion will be needed so that all can see
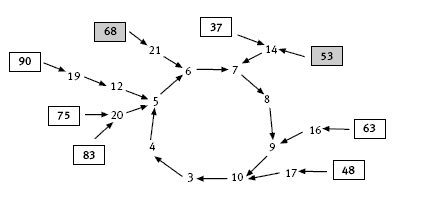
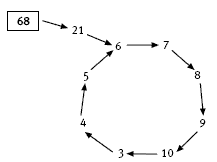
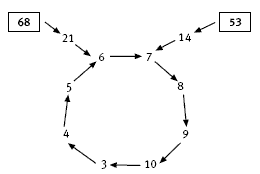
how, for example, 68 can be transformed into 21 and then to 6 and so on.
The interesting and surprising aspect of working with digit chains, which are easily made by devising a rule for each digit, is that they often reduce to a number that is part of a loop. The digit rules for question 1 produce a loop comprising the sequence 3, 4, 5, 6, 7, 8, 9, 10, 3, 4, 5, … The loops given in the Answers show how the digit rule works for the starting numbers 68 and 53.
In question 1c, the students create a separate digit chain for each starting number. When this is complete, they try to combine their separate digit chains so that they can clearly see the effect of the digit rule.
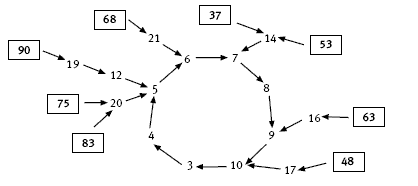
Note that three of the given starter numbers, 75, 83, and 90, all enter the loop at 5. The students could explore other 2-digit starters to see how many they can find entering the loop at 5. They might also do this for other numbers in the loop.
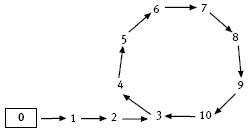
Before the students begin question 1e, they might try to predict what happens to 0, 1, and 2, which are not in the loop. As shown in the Answers, they will find that they form a separate string or sequence of numbers, which enter the loop at 3.
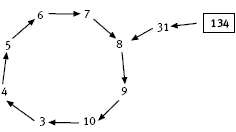
In question 2, the students extend their exploration of digit chains with the given rule to 3- and then 4-digit starter numbers. A diagram for 134 is:
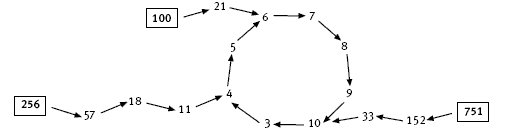
The 3-digit numbers enter the loop in the following way:
In question 2e, the students try to show how a 4-digit number they choose fits into the chain. The process may involve a number of steps, each of which provides an opportunity for the students to show their place value knowledge and their skills in working with numbers. For example, 26 384 is 2 638 tens and 4 ones.
So it becomes (2 x 2 638) + (4 + 1) = 5 276 + 5, which is 5 281. This becomes
(2 x 528) + (1 + 1) = 1 056 + 2, which is 1 058. And 1 058 becomes (2 x 105) + (8 + 1) = 219, which becomes (2 x 21) + (9 + 1) = 52. The number 52 becomes (2 x 5) + (2 + 1) = 13, which finally becomes (2 x 1) + (1 + 3) = 6 where it enters the loop.
Answers to activity
1. a.
b. i.–ii.
c. i. The digit chain for 37 is: 37, 14, 7, 8, 9, 10, 3, 4, 5, 6, 7, 8, 9, 10, …
The digit chain for 48 is: 48, 17, 10, 3, 4, 5, 6, 7, 8, 9, 10, 3, 4, 5, …
The digit chain for 63 is: 63, 16, 9, 10, 3, 4, 5, 6, 7, 8, 9, 10, 3, 4, …
The digit chain for 75 is: 75, 20, 5, 6, 7, 8, 9, 10, 3, 4, 5, 6, 7, 8, …
The digit chain for 83 is: 83, 20, 5, 6, 7, 8, 9, 10, 3, 4, 5, 6, 7, 8, …
The digit chain for 90 is: 90, 19, 12, 5, 6, 7, 8, 9, 10, 3, 4, 5, 6, 7, 8, …
ii.
d. Each 2-digit starter reduces to a number in the never-ending loop, 3, 4, 5, 6, 7, 8, 9, 10, 3, 4, …
e. Using the digit rule, 0 stays as 0 and begins the chain 0, 1, 2, 3, 4, … So, starter number 1 begins the chain 1, 2, 3, 4, 5, … , and starter number 2 begins the chain 2, 3, 4, 5, 6, … The diagram below shows how this works.
2. a. 134 = 13 tens and 4 ones. So 134 becomes (2 x 13) + (4 + 1) = 26 + 5, which is 31.
b. The number 31 becomes (2 x 3) + (1 + 1). 6 + 2 = 8, so 134 enters the loop at 8.
c. The starter number 100 is 10 tens + 0 ones. This becomes (2 x 10) + (0 + 1) = 21. Then 21 becomes 6, which is where it enters the loop. The starter number 256 is 25 tens + 6 ones. This becomes (2 x 25) + (6 + 1) = 57. Then 57 becomes 18, which becomes 11, which becomes 4, which is where it enters the loop. The starter number 751 is 75 tens + 1 one. This becomes (2 x 75) + (1 + 1) = 152, which
becomes (2 x 15) + (2 + 1) = 33, which becomes 10, which is where it enters the loop.
d. 2 138 = 213 tens and 8 ones. So 2 138 becomes (2 x 213) + (8 + 1) = 435, which becomes (2 x 43) + (5 + 1) = 92, which becomes (2 x 9) + (2 + 1) = 21, which becomes (2 x 2) + (1 + 1) = 4 + 2 = 6, which is where it enters the loop.
e. Answers will vary.
68
21