Decimals to tenths

Students would benefit from previous experience with fractions, particularly using partitioning of areas to form equal parts and the naming of collections of those as non-unit fractions. This unit uses a length model that is based on linear scales for whole number place value, such as rulers or kitchen scales. As a precursor to this unit, students should understand whole number place value in a flexible way. They should see place value as a nested system, meaning that, place value units (for example, tens) are nested in others (hundreds). For example, 230 can be renamed as 23 tens. It is also expected that students will have developed a range of strategies for solving addition and subtraction problems with whole numbers, including using standard place value (hundreds, tens and ones, etc.) and tidy numbers (rounding and compensating).

Session One

1. Use PowerPoint One to introduce the concept of temperature. Discuss body temperature and how it is measured using a thermometer. If possible, show students a range of thermometers (or images of them). You may want to use the opportunity to discuss “running a temperature” as a sign of infection and the average body temperature. Consider the following points as you progress through the PowerPoint:
   • What do students know about decimals temperatures?
   • Can they read the decimals correctly? For example, 36.8⁰C as “Thirty six point eight degrees Celsius.”
   • Can they locate decimals to one place on a scale? For example, recognise that 36.8 lies between 36 and 37.
   • Do they know the names of the places to the right of zero, tenths, hundredths, …?
2. Slides 5-9 provide opportunities to read temperatures on a thermometer. Point out that there are two main scales used in everyday life, Celsius and Fahrenheit. In New Zealand we use Celsius but other countries, notably the USA, use Fahrenheit.  Students might be interested to see how the scales differ - this could be explored using a digital tool (search for interactive temperature thermometer).
3. Discuss gradations on the scales, and what measure each mark corresponds to. Zooming into the graphic on Slide 5 shows that the fluid in the thermometer is at a level that is not an exact number of degrees.
   The red line appears to be a bit less than 30⁰C. What temperature might it be?
   The blue line appears to be below ⁰C. What temperature might it be? (negative integers appear on temperature scales)
4. For each of Slides 6-9 ask students to write what they believe the temperature is in each location. You could ask students to view these slides with a partner, and record their thinking to share with the class. Look carefully at the gradations and ask students how they will deal with the examples where the temperature is not exactly on a mark.
   Consider: Do students suggest decimal temperatures with an understanding of the size of the numbers they suggest?
5. Provide students with Copymaster One to work from in pairs. You could adapt this Copymaster to feature towns near to your area, to feature locations that are relevant to your current learning in other curriculum areas, or to feature areas your students whakapapa to. As they work, roam and look for the following:
   • Do students use the marks and measures on the scale to approximate the temperature and where to draw the bar? (Be aware that students are often unsure about how the units join end-on-end to create the scale, and whether the marks are at the end of the units (correct) or in the centre of the units (incorrect))
   • Do students show some understanding of decimals when they record temperatures? For example, they record 16.9⁰C for almost 17⁰C.
6. After an appropriate time gather the class to share answers and emphasise the points above.
7. Use Slides 10-12 of PowerPoint One to illustrate how the fluid (usually mercury or alcohol) rises in the thermometer as temperature increases. Extend counting in ones to counting in tenths.
   • Do students recognise that the smaller divisions are tenths, created by partitioning a length of one into ten equal parts?
   • Do they understand that ten tenths make one which is why whole numbers are collections of ten tenths?
   • Can they count in tenths past one, i.e. 1.1, 1.2, 1.3 …?
   • Note that the thermometer model is far from perfect since zero degrees is not the absence of quantity. It is simply a point on the scale that we measure from and that choice is based on the freezing temperature of water.

Session Two

In this lesson students create their own linear model for length, in ones and tenths. They learn the place value structure of the decimals.

1. Use Slides 1-3 of PowerPoint Two to refresh students’ memories about counting forward and back in tenths. 
   Model saying the decimals correctly and encourage students to do so. For example, 1.5 is spoken as “One point five” and 0.8 is spoken as “Zero point eight.” Emphasise that correctly reading decimal numbers is important because it recognises the different place values of numbers after the decimal point. 1.32 is one point three two, not one point “thirty two”, because the numbers after the decimal point are not “thirty two” - they are three tenths and two hundredths.
2. Use Slides 4 and 5 to illustrate counting forwards and backwards in tenths from a given decimal.
3. Show students how the constant function on a four-function calculator can be used to count in tenths. Many virtual forms of a simple calculator are available online (Search: Virtual Simple Calculator). Emphasise that 0.1 is the decimal for one tenth.
   • Key in + 0.1 = and keep pressing the = button. The calculator counts forwards in units of 0.1.  Students can count along. Pay special attention to the whole numbers and why there is no decimal point showing as the whole numbers come up.
   • Key in 3 + 0.1 = and keep pressing the = button. The calculator counts forwards in units of 0.1 from 3.
   • Key in 2 – 0.1 = and keep pressing the = button. The calculator counts backwards in units of 0.1 starting at 2.
4. Provide a calculator for each pair of students. Show how one student can provide a counting challenge for their partner. For example:
   Train your calculator to count forwards in tenths from 6.4. Predict the numbers before you press = .
   Train your calculator to count backwards in tenths from 6.4. Predict the numbers before you press = .
5. A significantly harder challenge is to predict how many units of one tenth are needed to reach a target decimal. For example:
   Train your calculator to count forwards in tenths from 2.8 but do not press equals. Hold your finger over the = button. Without looking press = until you reach 3.6. How many times did you press =?
   Train your calculator to count backwards in tenths from 7.4 but do not press equals. Hold your finger over the = button. Without looking press = until you reach 6.1. How many times did you press =?
6. Let students practise forwards and backwards counting in tenths with their partner. You may make this activity part of a daily routine until it is mastered.
7. Introduce a physical length model for decimals. Ideally use Cuisenaire Rods to make the model but Copymaster Two can be used to make a paper version. In the Cuisenaire version an orange rod becomes one (whole).
   Which rod is one tenth? How do you know?
   With the paper version discuss why the smaller lengths are labelled either 1/10 or 0.1.
8. Construct a thermometer scale on the mat using a strip of butchers’ paper. Use orange rods, or the paper one units, to mark the whole numbers by placing units end on end.
   
9. Ask students to build decimals that are between whole numbers, such as 2.5⁰C and 0.8⁰C. Create the physical models and locate the decimals on the thermometer. Focus the discussion on the composition of each decimal. For example, 2.5 is composed of two ones and five tenths.
10. Give the students a set of temperatures to locate on a thermometer they create using either the Cuisenaire Rods or paper version. Provide them with paper strips and felt pens and ask them to work in pairs. A good set of temperatures might be:
    1.5⁰C   3.8⁰C   0.3⁰C   2.7⁰C   0.9⁰C   1.8⁰C      4.1⁰C   2⁰C     
    The location of these on a thermometer could be modelled using a class model or digital tool (search for interactive temperature thermometer).
11. Roam the room as students work, looking for the following:
    • Do students read the decimals correctly?
    • Can they explain the place value structure, that is, how many ones and tens make up the number?
    • Are they able to predict the location of the number before making it with materials?
12. Display the thermometers on the wall of your classroom.

Session Three

In this lesson students use their knowledge of decimal counting and place value to add and subtract decimals with one decimal place.

1. If possible, bring in a fishing sinker that is used to keep the line below the surface. Pass the sinker around.
   What is this sinker made from?
   Why is it made from lead?
   Ice melts. Does lead melt?
2. Record the number 327.5 ⁰C on the board.
   This is the temperature that lead melts at. How might you get a temperature that hot?
   Some ovens can reach temperatures that high, and students might suggest blow torches and other devices used to melt metals.
   What can you tell me about the place values of 327.5?
   Draw attention to the hundreds, tens, ones and tenths places. Make links back to learning from the previous two lessons, or to the temperature if your local area, to consolidate understanding of tenths (For example, Remember we looked at the temperature in different areas - it was 3.9⁰C in Ohakune - 3.9 is made up of 3 and 9 tenths).
   
3. Use PowerPoint Three, Slides 1 to 3 to introduce the addition of one place decimals in the temperature context. Use think, pair, share for each problem. Students firstly need to establish the temperature reading as a decimal before adding the gain.
   Do your students recognise the problems as addition, since two amounts are joined? 
   Can they estimate the answer, in terms of being larger or smaller than a whole number (or equal)?
   Expect students to justify their answers using the language of place value.
4. Record the solution to each problem as equations and vertical algorithms. In doing this, make links to the addition strategies that your students are confident using:
   • Slide 1: 0.8 + 3 = 3.8
   • Slide 2: 1.3 + 2.7 = 4
   • Slide 3: 1.9 + 1.5 = 3.4
     
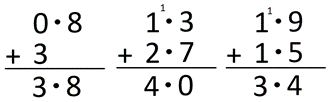
5. Provide students with Copymaster Three to work from in pairs. Allow students access to the Cuisenaire Rod or Paper model to support their thinking if needed. Calculators can also be provided to students to check their answers, but not for the initial calculation.
6. Roam the room as students work. Look for the following:
   • Do students demonstrate understanding of the place value structure of the numbers?
   • Do they recognise that when ten or more tenths are combined another one is formed?
   • Do they use efficient strategies and recording to support their calculations?
   • Do they recognise, if more tenths are required in a subtraction, a one must be decomposed into ten tenths?
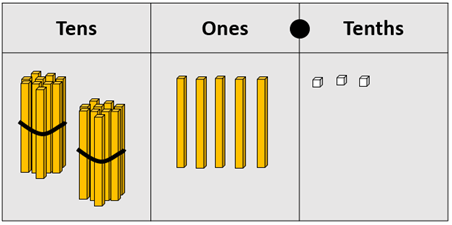
7. Allow sufficient time for students to work through the problems and discuss selected examples that bring out the points above. Since many of the temperatures are above ten you may want to use a place value board to organise the calculations. Here is how a temperature of 25.3⁰C can be shown using the Cuisenaire model. If necessary, begin with a linear representation with the rods end on end and move them into this column representation.
   
8. Establish some standardised algorithms for adding and subtracting decimals to one place.  If your students are not familiar with standardised algorithms, spend some time scaffolding them to successfully use these to show the addition and subtraction of whole numbers. Ensure that the procedures are founded on place value knowledge through the initial use of the Cuisenaire or paper strip model. Not that ten one strips can be fixed together to form a ten using a staple or paper clip. Alternatively, draw on students’ knowledge and utilise other strategies to model adding and subtracting decimals (e.g. using a number line, combining and partitioning, tidy numbers).
9. Consider the example of Kawakawa, that increases in temperature by 5.9⁰C from 11.8⁰C. The addition might be modelled as:
   
   
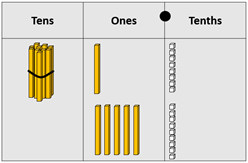
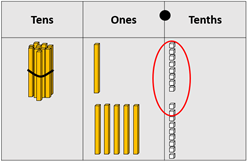
   Adding 2 tenths to 11.8 creates another one.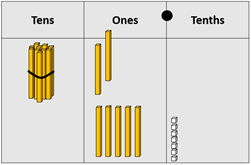
   
   
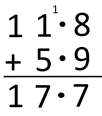
   The result equals 17.7⁰C. As an algorithm the calculation can be recorded vertically.
   Some students may use efficient mental strategies such as:
   “Exchange two tenths between 11.8 and 5.9 to create 12 + 5.7 that can be solved without renaming, 12 + 5 = 17 so 12 + 5.7 = 17.7.”
10. Similarly, the example of Castlepoint involves the subtraction 14.1 – 4.8 = 9.3⁰C that also requires renaming. The calculation might be modelled in this way:
    
    
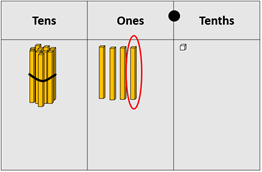
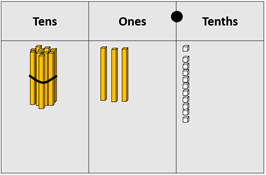
    Subtracting 8 tenths requires decomposition of a one unit to create 13 ones and 11 tenths.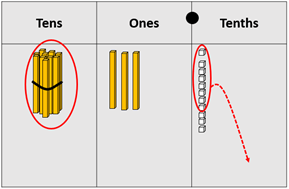
    
    
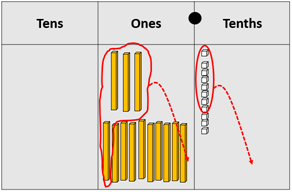
    8 tenths can be subtracted, leaving 13.3. One ten must be decomposed so 13.3 is renamed as 13 ones, and 3 tenths. 4 ones can be subtracted leaving 9.3⁰C. As a vertical algorithm this is: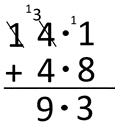
    

Session Four

The aim of this session is to consolidate addition and subtraction of decimals using place value understanding that has been built up over the previous three lessons.

1. Begin with the first three Slides of PowerPoint Four that contain difference problems. The problems can be solved either by adding on or subtracting. Students sometimes have difficulty with problems of this type because the action is not explicit in the problem statement.
2. With each problem let students work in pairs or threes. Be open to a variety of mental and written strategies, such as using standard place values, rounding, and compensating, and jumping through tens and ones. Encourage students to record their working to ease mental load, use Cuisenaire or paper materials if needed and to check their calculations with a peer and a calculator. Below are some points to highlight.
   • Alexandra and Castlepoint 
     Rounding and compensating: 20 + 14.5 = 34.5 so 19.8 + 14.7 = 34.5⁰C (adding 2 tenths)
     Using place value: Rename 34.5 as 33 and 15 tenths. 15 tenths subtract 8 tenths leaves 7 tenths and 33 – 19 = 14. So, the difference equals 14 + 0.7 = 14.7⁰C.
   • Kaitaia and Levin
     Place value: 6 tenths subtract 3 tenths leaves 4 tenths. 28 subtract 19 equals 9. So, the difference equals 9 + 0.4 = 9.4⁰C.
     Jumping through tens and ones: 19.2 + 0.8 = 20, 20 + 8.6 = 28.6. Combine the jumps gives 0.8 + 8.6 = 9.4⁰C.
   • Tolaga Bay and Invercargill
     Rounding and compensating: The difference between 12.7 and 32.7 equals 20. 32.7 is 1.1 more than 31.6. So, the difference between 12.7 and 31.6 equals 20 – 1.1 = 18.9⁰C.
     Standard place value: Rename 31.6 as 30 + 16 tenths. 16 tenths subtract 7 tenths equals 9 tenths. 30 subtract 12 equals 18. So, the difference equals 12 + 0.9 = 12.9⁰C.
3. As well as written algorithms, use empty number lines to record calculations. Below is one example of adding on to solve the difference between 12.7 and 31.6.
   
4. Use Copymaster Four to provide students with two puzzles, one involving addition (finding sums), and the other involving subtraction (finding difference). Students can just use a paper form of the puzzles and cut up the cards. Alternatively, you can laminate the puzzle cards for long term use.
   Below are instructions. Use PowerPoint Four, Slides 4 and 5 to introduce the puzzles. Note that the numbers on the PowerPoint are different to the puzzle cards:
   • Lay the city cards out in a square arrangement with lots of space between cards.
   • Place all six “sum” cards in the correct position (vertical, horizontal, or diagonal) so that the sums match the temperatures of the cities.
   • Once the sum cards are completed and checked, do the same thing with the six difference cards.
     Roam the room as students work on the puzzles in pairs or small groups. Look for the following:
     • Do students use sensible rounding to the nearest whole number to find approximate sums and differences?
     • Do they look for appropriate digits in the tenths place? For example, a sum that has 3 tenths must involve tenths digits in the addends that add to 3 or 13.
     • Do they understand that difference can be found by adding on or by subtracting?
5. After a suitable time gather the class together to discuss the strategies used.
   What did you look for when you worked on the puzzles?
   How did you know where best to put an arrow card?

Session Five

In this session students are given the opportunity to demonstrate their understanding of decimals to one place.

1. Provide each student with Copymaster Five. Ask them to attempt the problems by themselves before sharing with a partner then the whole class. Calculations can be done mentally or with pen and paper. Calculators might be used later to check answers.
2. Roam as the students work, clarifying instructions if needed.
3. Use the questions to check students’ understanding and procedural fluency as follows:
   • Question 1: Do students mark the level as about one quarter of the distance between 20 ⁰C and 30 ⁰C?
   • Question 2: Do students model the problem with 9.7 + 8.5 = 18.2 ⁰C?
   • Question 3: Do students model the problem with 35.4 - 12.6 = 22.8 ⁰C?
   • Question 4: Do students recognise the the problem is asking them to find the difference, and solve it using 23.6 – 18.9 = 4.7 ⁰C or 18.9 + 4.7 = 23.6 ⁰C?
   • Question 5: Do students locate the temperature at approximately correct points on the scale?
     
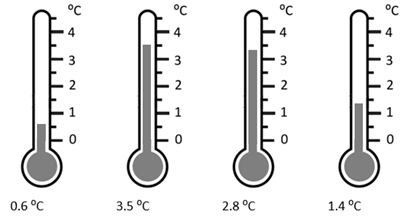
   • Question 6: Do students satisfy both clues, possibly by trial and improvement, to find the temperatures are 10.3 ⁰C and 13 ⁰C?
   • Question 7: Do students recognise that the temperature difference stays constant if both temperatures increase by the same amount?