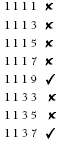Dates and Shapes

Problem One

The students need to think first about what odd numbers they can use. They can use 1, 3, 5, 7, and 9, but they can’t use 11 or above because adding three more odd numbers will give a total higher than 12.
The best strategy is to start with three ones and work systematically. Some students may need to write down all the options and cross out those that do not work, for example:

Encourage the students to move as quickly as possible to a list of only those that do add up to 12, by adding in their heads as they go and leaving out those that do not fit the criteria.
They will then end up with a list of five:
1 + 1 + 1 + 9
1 + 1 + 3 + 7
1 + 1 + 5 + 5
1 + 3 + 3 + 5
3 + 3 + 3 + 3

Problem Two

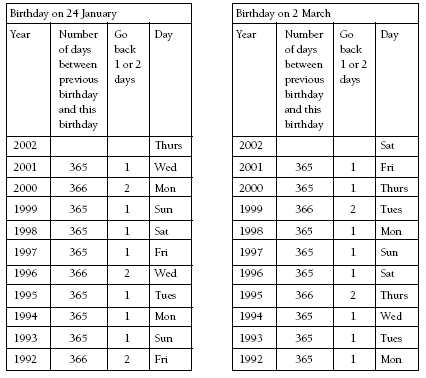
To solve this problem mathematically, students need to work out how the days of the week change for a certain date in preceding years. (The other way to solve the problem is to look up a calendar for the year they were born at a library or on the Internet. Once the students have solved the problem mathematically, they could use this alternative method to check their answer.)
Working out how days change from year to year would be simple if it weren’t for leap years. In an ordinary year, there are 365 days, which is 52 weeks and 1 day. So from one non-leap year to the next year that is also a non-leap year, any date will be one day of the week later. For example, 2 March 2001 is a Friday; 2 March 2002 is a Saturday. Conversely, going from one non-leap year back to the previous year that is also a non-leap year, any date will be one day of the week earlier.
For example, 24 January 2002 is a Thursday; 24 January 2001 is a Wednesday.
Leap years occur every year that is a multiple of 4. Leap years are 366 days long or 52 weeks and 2 days. The extra day is 29 February. So for birthdays on or before 28 February, moving forwards from a non-leap year to a leap year, the day of the week will move forward by 1 day. This is because they have not yet got to the extra day in the year (29 February). Moving from a leap year to a non-leap year, the day of the week will move forward by 2 days. This is because the leap-year birthday is before the extra day (29 February).
For birthdays on 1 March and after, moving from a non-leap to a leap year, the day of the week will move forward by 2 days because the leap-year birthday is after the extra day (29 February). Moving from a leap to a non-leap year, the day of the week will move forward by 1 day because the extra day (29 February) occurred before the leap-year birthday. As above, these rules are reversed when working backwards.
Another way of looking at this is asking “Is there a leap day (29 February) in the 1 year period from one birthday to the next?” If yes, the day of the week will move forward by 2 days. If no, the day of the week will move forward by 1 day. Working backwards, if there is a leap day in the 1 year period from one birthday to the previous birthday, the day of the week will move back 2 days. If there isn’t a leap day in the 1 year period from one birthday to the previous birthday, the day of the week will move back 1 day.
Below are examples of the changing days for a birthday before and a birthday after 28 February for people born in 1992.

Note that for birthdays on or before 28 February, the day of the week moves back 2 days on the leap year, but for birthdays on or after 1 March, the day of the week moves back 2 days the year before the leap year.
The students will need to work very carefully through this problem because of the effect of a leap year. Those who were born on 29 February will have to decide whether they celebrate their birthday in non-leap years on 28 February or 1 March.

Problem Three

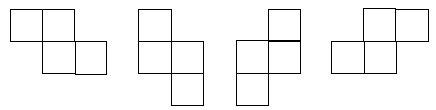
a. There are only five tetrominoes that can be made without involving reflection or rotation. Examples of these are shown in the Answers. The students may have reflections or rotations of these shapes and think that they are different tetrominoes. You may need to show them that they are actually the same as one of the tetrominoes given in the Answers. For example, the following shapes are all the same tetromino under rotation or reflection:

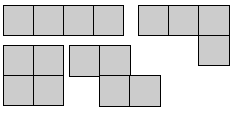
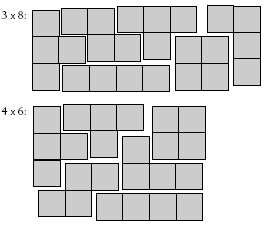
b. The six tetrominoes combined will give 24 squares (4 x 6 = 24). So the rectangle could have dimensions of 1 x 24, 2 x 12, 3 x 8, or 4 x 6. Some of the tetrominoes take up two rows, so you can’t make a 1 x 24 rectangle. A 2 x 12 rectangle is also not possible. Experiment, and you will see why. The only two rectangles left with 24 squares are 3 x 8 and 4 x 6. These are shown in the Answers.

Problem Four

This problem can be solved very simply. The solution is outlined in the Answers.

Hints for Students

1. Think carefully about all the numbers you can use and then work systematically.
2. What do you need to know? How many days are there in a year? What happens in leap years?
3. Use a diagram, or use equipment to find different-shaped tetrominoes.
Then experiment (but work systematically) to make the rectangle.
4. Try a smaller case first. For example, how can you measure 2 litres with these buckets?

Answers to Problems

1. Possible answers are:
1 + 1 + 1 + 9
1 + 1 + 3 + 7
1 + 1 + 5 + 5
1 + 3 + 3 + 5
3 + 3 + 3 + 3
2. One way of doing this is to track back. You need to know how many days are in each year (including leap years) and how the days change from year to year.
3. a.

b. You can have a 3 x 8 rectangle or a 4 x 6 rectangle. One way of constructing each of these is shown below.

4. Step 1: Fill the 7 L bucket.
Step 2: Fill the 5 L bucket from the 7 L bucket. (There is now 2 L remaining in
the 7 L bucket.)
Step 3: Empty out the 5 L bucket.
Step 4: Empty the 2 L in the 7 L bucket into the 5 L bucket.
Step 5: Refill the 7 L bucket.
Step 6: Top up the 5 L bucket from the 7 L bucket. (This will take 3 L of water,
which means 4 L remain in the 7 L bucket.)