This problem solving activity has a number focus.
The twins each have three darts and a dartboard with three rings.
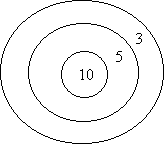
Here is Hana's board. What possible totals can she score if all of her darts land on the board?
Here is Henri's board. Not all of the numbers on his are the same as on Hana’s.
The possible totals that Henri can make are 9, 11, 13, 15, 16, 18, 20, 23, 25, 30.
What numbers are on Henri’s board?
- Identify and describe patterns in numbers.
- Use expressions and words to describe number patterns.
- Devise and use problem solving strategies to explore situations mathematically (be systematic).
This problem gives students the opportunity to be systematic in the way they combine numbers, be alert to number patterns, and to express patterns in simple expressions and with the use of their own language.. The challenge is to see what scores can be made.
Similar Number problems include: Darts, Level 3; Super darts, Level 3; and More Dartboards, Level 4.
The Problem
The twins each have three darts and a dartboard with three rings.
Here is Hana's board. What possible totals can she score if all of her darts land on the board?
Here is Henri's board. Not all of the numbers on his are the same as on Hana’s.
The possible totals that Henri can make are 9, 11, 13, 15, 16, 18, 20, 23, 25, 30.
What numbers are on Henri’s board?
Teaching Sequence
- Introduce the problem with a discussion about the game of darts.
- Display or draw Hana's board and have students identify the highest score that can be obtained from throwing three darts.
- In pairs ask the students to find all the possible scores obtained from throwing three darts.
- Share the possible scores.
- Pose Henri's problem for the students to work on. Check that they understand what is required.
- As they work, ask questions that focus on their manipulation of numbers using the number operations. Encourage them to justify their solutions.
How did you begin? Why did you start there?
How did you work out the numbers?
What information was the most useful? Did you need it all?
Can you see any patterns in the numbers?
Could you write an expression to show this pattern?
Are you working systematically? How? How could you be more systematic?
What do you still need to work out?
Are you convinced you have the solution? Might there be another one? Why or why not? - As the students work, encourage them to record their solutions so that they can be shared with others in the class.
- Share solutions.
Extension
Suppose that you had a board something like Hana’s and Henri’s but with not necessarily the same numbers. How many possible totals could you get by using three darts?
Could any two of these totals be the same?
Solution
Using a systematic approach on Hana’s board:
The darts might all fall into the same number ring; two might be the same and one different; and all the numbers might be different. So the totals would be:2 + 2 + 2 = 6 5 + 5 + 5 = 15 9 + 9 + 9 = 27 2 + 2 + 5 = 9 2 + 2 + 9 = 13 5 + 5 + 2 = 12 5 + 5 + 9 = 19 9 + 9 + 2 = 20 9 + 9 + 5 = 23 2 + 5 + 9 = 16 This gives ten totals: 6, 9, 12, 13, 15, 16, 19, 20, 23, 27.
- For Henri’s board. If 3 darts ‘hit’ the same region then the totals will be a multiple of 3. Now we could look for the numbers among the list that are divisible by 3. There are four of these and there are only three totals that can be made by using the same number twice.
The smallest number will be a multiple of 3 because that is the smallest number on the board hit with three darts. Since the smallest number is 9, then the smallest number on the board is 3.
The biggest number has to be a multiple of 3 too. Since the biggest total is 30, the biggest number is 10.
How can we get the other number from Henri’s board? What is the next smallest total? It is formed by adding two of the smallest number on the board to the middle number on the board?
11 = 2 x 3 + the middle number.
This problem provides more information than is needed.
Solution to the Extension
Suppose that the three numbers were a, b and c. Then we could list the totals in the same way that we listed the totals on Hana’s board.
- Three the same: 3a, 3b, 3c.
- Two the same: 2a + b, 2a + c, 2b + a, 2b + c, 2c + a, 2c + b.
- All different: a + b + c.
This gives 10 possible totals. This is at least consistent with the two examples that we’ve had so far.
Could any of these 10 totals be the same? Let’s assume that a < b < c, otherwise there are going to be lots of totals that are the same.
3a must be different from any other total since a is the smallest number.
Similarly 3c must be the biggest number.
What happens to 3b? Is it clear that 3b isn’t equal to any of 2a + b, 2b + a, 2b + c or 2c + b? So let’s try putting 3b = 2a + c. We’ll do this using an example. Try a = 5 and c = 11. Then b = 7. So what totals do we get with 5, 7 and 11 on the board?
- Three the same: 15, 21, 33.
- Two the same: 17, 21, 19, 25, 27, 29.
- All different: 23.
So here there are only 9 totals. These are 15, 17, 19, 21, 23, 25, 27, 29, 33.
Must we always get at least 9 different totals?

