This unit encourages students to compare quantities both additively and multiplicatively.
- Describe multiplicative comparison between two quantities using appropriate language, such as, “three times more/greater/bigger”, “three times less/smaller.”
- Record multiplicative comparisons using equations, such as, 4 x 3 = 12 (for 12 is four times greater than three).
- Find the unknown scalar between two quantities using multiplication and division, such as the multiplier between 6 and 24 is 4 because 24 ÷ 6 = 4.
Multiplicative comparison between two quantities is significant to the future success of students, particularly for their understanding of proportions. Consider two quantities, such as five and fifteen. How can the two quantities be compared?
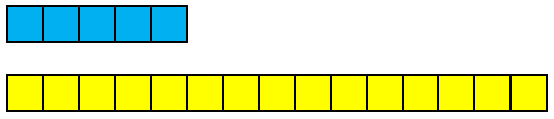
Here are some things that could be said:
- 15 is 10 more than 5
- 5 is 10 less than 15
- 15 is three times as much as 5
- 5 is one third as much as 15
The top two statements are additive comparisons that can be made about the difference between 5 and 15. The bottom two statements are multiplicative comparisons that can be made about the scalar between 5 and 15. You can think of the scalar as a multiplier.
Finding the scalar is simple with numbers like 5 and 15 as facts like 3 x 5 = 15 are commonly known. When the numbers are more complex, students need an algorithm to find the scalar. If you ask, “How many times does 5 fit into 15?” you establish that the scalar between 5 and 15 is 3.
You could write the algorithm as 15 ÷ 5 = □ to find □ x 5 = 15.
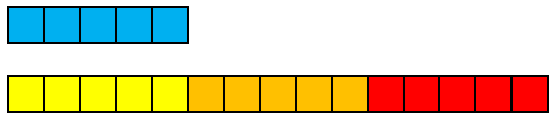
The scalar between 5 and 15 is a more difficult relationship since it is a fraction. Let’s apply the same algorithm as above. If you ask, “How many times does 15 fit into 5?” you realise that the scalar must be a fraction less than one. Since five is one third of 15, the scalar is one third.
You could write the algorithm as 5 ÷ 15 = □ to find □ x 15 = 5. Note that a common misconception students hold about division is that the divisor is always less than the dividend. In this case the divisor, 15, is greater than the dividend, 5.
The learning opportunities in this unit can be differentiated by providing or removing support to students and by varying the task requirements. Ways to differentiate include:
- providing physical materials so that students can anticipate actions and justify their solutions. Linear models, like connecting cubes, are preferred. Use colours to show how many times the measurement length fits into the target length
- connecting symbols and mathematical vocabulary, especially the symbols for multiplication and division (x, ÷) and for equality (=). Explicitly model the correct use of equations and algorithms, and discuss the meaning of the symbols in context
- altering the complexity of the numbers that are used. Scalars (multipliers) that are whole numbers are much easier than fractions, e.g. □ x 9 = 36 is much easier than □ x 9 = 6
- encouraging students to collaborate in small groups and to share, and justify, their ideas
- using technology, especially calculators, in predictive, pattern-based ways to generalise how scalars can be found using division. Use of calculators broadens the range of numbers accessible to all students
The context used for this unit involves lengths of tuataras, scores in a top student competition, ages, fish, and price inflation. Using a range of situations helps to engage students and helps them to see application of mathematics to the real world. Vary the contexts to suit the cultures and interests of your students while retaining the mathematical focus of the unit. You might compare improvements in kapa haka scores, changes in points scored in sport, number of whānau members at a marae gathering, or distance of houses from school. Ask students to choose the objects that appeal to them, in comparing 1991 and today’s prices.\
Te reo Māori vocabulary terms such as whakatairite (compare), iti iho (less than), nui ake (greater than) and whakarea (multiply/multiplication) could be introduced in this unit and used throughout other mathematical learning.
- Calculators
- Linking cubes
- PowerPoint 1
- Powerpoint 2
- PowerPoint 3
- Copymaster 1
- Copymaster 2
- Copymaster 3
- Copymaster 4
Session 1
The context for this session could be altered to focus on animals that have significance in your local area. For example, in Ōtepoti (Dunedin) little blue penguins or albatross may hold more interest for students. The picture book Wildlife of Aotearoa by Gavin Bishop (2019) could be used to ignite students’ interests in this context.
- Begin with a growth problem (see PowerPoint 1 ).
Tuati and Tera are tuatara lizards. They are small reminders of a time when dinosaurs ruled the Earth.
Nowadays scientists measure tuatara to check that they are growing well, as they are an endangered species.
In 2000 Tuati was 10 centimetres long and Tera was 16 centimetres long.
This year Tuati is 30 centimetres long and Tera is 40 centimetres long.
Which tuatara grew the most between 2000 and today, Tuati or Tera?
- You may like to make four models of the tuatara using linking cubes and arrange them in this way:
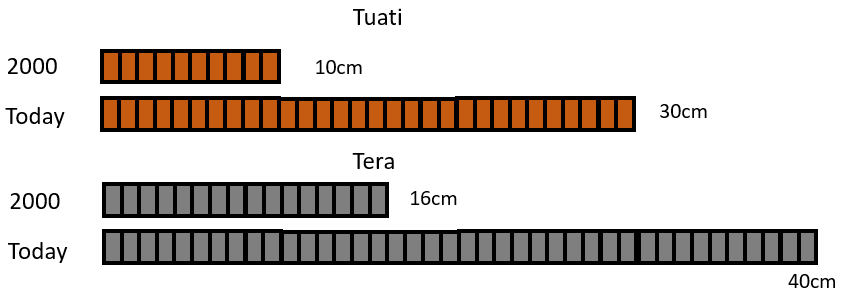
- Let your students work in small groups to answer the question. Encourage them to rehearse the strategy they used so they are ready to share it with the whole class. After an appropriate time, bring the class together for discussion.
Some students, possibly most, will use additive comparison. They will find the number of centimetres each tuatara grew in the time. Highlight that they have found the differences between the today and year 2000 lengths. The difference can be found either by ‘adding on’, or subtracting. For example:
I added on from 16 until I got to 40. That was 24 centimetres growth for Tera.
I subtracted 10 from 30 and got 20 centimetres for Tuati.
- You may choose to use empty number lines to record the calculations.
Finding the difference is a legitimate way to compare the growth of the two tuatara. That will lead to the conclusion that Tera grew more than Tuati. However, a multiplicative comparison leads to another conclusion.
How many times as long is Tuati today than he was in the year 2000?
How many times as long is Tera today than she was in the year 2000?
The term ‘times as long’ needs explanation and representation. Use PowerPoint 1 to illustrate the concept. Tuati is three times as long as he was in 2000, and Tera is two and one half times longer than she was. The comparison of 40 with 16 requires students to recognise 16 as the unit of comparison, and express the eight cubes in the third iteration (repeated copy) as one half of 16. You might record the relationships using equations;
3 x 10 = 30 2½ x 16 = 40
- Provide the students with Copymaster 1 which contains a variety of tuatara growths between 2000 and today. Students can work together, utilising the tuakana-teina relationship between more and less knowledgeable students, to establish the ‘times as long’ relationship for each tuatara. If needed, provide linking cubes and fraction strips so students can form the two lengths and map the year 2000 length into the today length.
- After sufficient time, bring the class together to share the answers. Pay attention, particularly to:
- Anticipation of the relationship by thinking about “How many times does x fit into y?”
- Noticing the need for fractions where the 2000 length does not map into the today length a whole number of times
- Situations where the tuatara has reduced length between 2000 and today so the multiplier is a fraction less than one.
Session 2
Multiplicative comparison sometimes requires a multiplier that is not a whole number. In this session students explore applying a whole number multiplier then extending their understanding to fraction multipliers.
- Start with simple problems where the multiplier is known. PowerPoint 2 provides a scenario of students getting points in a ‘Top of the class’ competition for taking care of each other. Links could be made here to your school values, or actions that show manaakitanga (care). Each odd numbered slide is a problem to solve. Use ‘think, pair, share” to give students the opportunity to solve each problem before turning to the even numbered slide that follows. Even slides illustrate how the ‘times as many’ relationship works using a linear cube model.
- Give each pair of students a small set of cubes. Ask them to build a model of each situation below:
Amy has three kiwis at Orokonui Ecosanctuary. Ben said he saw three times as many. How many kiwis did Ben see?
The korimako laid 2 eggs. The Tuī laid eight times as many. How many eggs did the Tuī lay?
When she was snorkelling, Kayla saw some beautiful spotted black grouper. Mike saw 15 spotted black grouper, , that’s three times as many as Kayla. How many spotted black grouper did Kayla see?
On their bushwalk Sam counted some pupurangi (flax snails). Lia spotted 20 pururangi, that’s two and one half times as many as Sam. How many pururangi did Sam spot?
Note that the last two examples involve an inverse operation. For example, Kayla and Mike’s situation might be recorded as 3 x □ = 15. Look to see if your students understand that the unit of comparison is mapped onto the other quantity a certain number of times. In Kayla and Sam’s situation they need to find a unit that maps into 15 three times.
- You might extend the problems to include fractional multipliers, depending on how students are progressing.
There are nine species of dolphins that can be found around New Zealand's coast. Fran thinks there are two thirds as many whales. How many whales does Fran think there are?
Ena spotted some Pūkeko during their class trip to the wetlands. Dan spotted 15 Pūkeko, that's one and one half times as many as Ena. How many Pūkeko did Ena spot?
- Record each problem as an equation. For example, the Ena and Dan situation is represented by 1½ x □ = 15.
- Finish the session with a complex problem that involves organising a lot of ‘times as many’ relationships. Copymaster 2 contains the problem. Let your students attempt the problem in small groups or pairs. Useful prompts might be:
- Which clue is the best to start with? Why?
- How can you organise the information to help take a load off your brain?
- Look at clue 3. What ages could Dad be? Why?
- Can you use that thinking to find other possible ages?
The solution is: Rex is four, Dave is six, Kate is nine, Mum is 36, Dad is 40, Nana is 66 and Pop is 72.
- Students might make up their own problems, for others to solve, using the ages of their family members or the ages of their favourite sports people and public figures. You could make a book of ages problems to put in the mathematics corner.
Session 3
In this session students identify the multiplier connecting two quantities. They learn that the multiplier can be found using division and use that knowledge to solve more complex problems than they can solve mentally. Calculators are used to increase the range of numbers accessible to the students.
- Use PowerPoint 3. Students should recognise that there are three times as many orange fish as blue fish on Slide 1.
What equation can you write for this problem?
- Let your students try to write an equation then share. Most will write a multiplication problem like this: □ x 4 = 12 or 3 x 4 = 12
Some may reverse the order of the factors, i.e. 4 x 3 = 12. In English speaking countries the multiplier is conventionally written as the first factor. Discuss what the 3 and 4 refer to in the equation. Four is the unit of comparison, the known set. Three is the multiplier that tells how many times 4 maps into 12. - How did you work out that the first factor was 3?
Some students may have skip-counted or scanned their four times multiplication facts to find the missing factor. It is possible some students used division, asking themselves “How many times does 4 fit into 12?”
- Write an equation for “How many fours are in 12?”
- Record the multiplication and division equations for the fish scenario: □ x 4 = 12 and 12 ÷ 4 = □
Note that 12 ÷ 4 = □ refers to measurement division (quotative) meaning “How many fours measure 12?” Use calculators to verify that 12 ÷ 4 = gives the multiplier, three.
- Move to Slides 2, 3 and 4 of PowerPoint 3 that increase in complexity. As the numbers become more difficult students should realise that using division has strategic advantage. Allow use of calculators after students attempt the problems mentally.
Look for students to recognise that if 3 x 4 = 12 then 9 x 4 = 36. Also encourage them to use known facts to solve complex problems. For example (Slide 3):
If there were blue fish, what would the ‘times as many’ factor be? (6 x 8 = 48)
How can you use that fact to work out □ x 3 = 48? (Twice as many threes as sixes measure 48)
- For each problem write multiplication and division equations to represent the solution.
- Complete the lesson with Copymaster 3 that contains calculator change problems. For example, "What single multiplication operation changes 6 into 48?"
Since 48 ÷ 6 = 8 the multiplier is eight and 8 x 6 = 48.
- After students complete Copymaster 3 share their strategies. Do they use division to find the unknown multiplier. To extend their thinking you might pose change problems that have fraction multipliers. For example: 6 → 57, or 24 → 18
Session 4
- Remind the students of the problems they investigated to date (tuatara lengths, top student points, tropical fish, calculator change). Ask them to write down features that are the same about all four problem sets. Encourage them to use examples of problems to illustrate their ideas.
- Discuss the comparison nature of all the problems. One quantity has been measured with another to see how many times it fits in. Expect students to also see that all the situations can be represented as multiplication and division equations.
- To see if you understand the ideas in this unit, I have another problem for you to solve. Have you heard of inflation? What does that mean?
You may need to explain that inflation is the increase in the price of things, from food to electronic devices to rent on houses. Statistics New Zealand uses a mixture of things to work out how much prices are increasing or decreasing. Be aware that discussions of money, renting/owning houses, and the cost of household items may be a sensitive topic for some of your students. The context to the learning in this session could easily be altered to compare the price of living in New Zealand to the price of living in other countries. Students could work in groups, with each group choosing a country to compare to New Zealand. - In 1990, about when your parents were born, the average rent for a house in Auckland was about $200 per week. Today, to rent the same house would cost at least $500 per week.
How much has the rent increased since 1990?
- Students might express the relationship between 200 and 500 as an increase of $300 or as “two and one half times as much.” Reiterate that the unit is about multiplicative comparison, “times as many” or “times as much.” Ask for the equations that represent the comparison (2½ x 200 = 500 or 500 ÷ 200 = 2½).
- Copymaster 4 has average prices for items in 1990 (source New Zealand Yearbook, 1991). Tell your students that their task is to work out how many times dearer each item costs today compared to the price in 1990. To help them, provide junk mail flyers from supermarkets and appliance stores. They could also access this information online. You could also use the New Zealand Yearbook for results from 1893-2012. This is easily accessible online (search: New Zealand Yearbook). Students will also need calculators as the numbers are not always friendly.
- Let your students work in small teams to find the multipliers. Watch for students using consistent units. Comparing prices may require them to convert dollar amounts into cents or vice versa. Do your students apply division to find the multipliers?
- After a suitable period, discuss what they have found out.
Are the increases consistent?
Why might some things increase more than others?
Which things increased the most? Which things increased by the least?
Students might notice that the stove and computer cost about the same number of dollars as they did back in 1990. Food items tend to be two to three times dearer, except for bananas that are about the same. Students at Level 3 are just beginning their learning of decimals so encountering numbers like 2.38 is an opportunity to discuss rounding, possibly with the support of a number line.
Dear family and whānau,
This week at school we are learning to solve “times as many” problems. Here is an example:
The problems we will solve will have more difficult numbers than that as we are working at becoming good at multiplication and division.