This problem solving activity has a measurement focus.
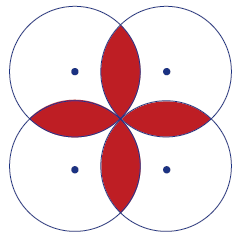
Dan makes a badge using his ruler and compass. He colours it red and white. This is his drawing. The centres of the circles lie at the corners of a square.
Construct your own version of Dan’s Badge.
Dan uses a radius of 10cm for his circles. What area of his badge is shaded red?
- Apply formulae for the area of squares and circles to solve problems.
In this problem students apply their knowledge of the formulae for the area of a square and a circle as they investigate a given design.
A simpler version of this problem is: Bill’s Badge, Measurement, Level 5.
The Problem
Dan makes a badge using his ruler and compass. He colours it red and white. His drawing is below. The centres of the circles lie at the corners of a square.
Construct your own version of Dan’s Badge.
Dan uses a radius of 10cm for his circles. What area of his badge is shaded red?
Teaching Sequence
- Pose the problem to the class. Have them think first about the construction, then share their ideas.
- List suggestions on the board.
- Have the students reconstruct Dans’ badge.
- As the students work on the construction, ask questions that focus on the measurements used and the relationships that they can see.
Do we need to be precise in our construction of Dan's badge? What shape attributes do we need to consider? - Share constructions and approaches used.
- Pose the second part of the problem. Remind the students to think about how they constructed the badge and how this will help in thinking about the areas.
- As the students work (in pairs) ask questions that focus on the known measurements in the problem and the relationship between these and the required area.
How do we know where the centre of the circle is?
How can we find the area of the square? - Ask the students to record their solution for others to read.
- Share solutions.
Solution
Construction: First construct a square. (There is no need to be too precise on the dimensions in this problem.) This can be done by marking off two points on a line and drawing perpendicular lines from these two points. Use dividers to measure the length between the two original points and mark this length off on each of the two perpendicular lines. Then join the two points so produced.
We now know where the centres of the circles are. To draw in the circles we need to know the radius on the diagram. We note that the four circles meet at the centre of the square. So draw in the two diagonals of the square. The radius of a circle is the distance between the centre of a circle and the point where the diagonals meet. Now the circles can be drawn to complete the diagram.
Area: There are many ways to find the area of the red part of Dan’s Badge. One way is to draw in the square shown in the diagram. To check that this is indeed a square, note that the side AX is half of the diagonal of the square that Dan started with. So this is at 45o to the side AB. AB goes symmetrically through the middle of the red part and so the angle of XAY = 90o.
The square has area 10 x 10 = 100 cm2 because the length of the side is the radius of the circle which is 10 cm.
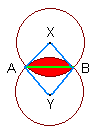
The sectors AXB and AYB are each 1/4 area of the circle = 1/4 π 102 = 25π cm2. Hence the area not dotted is 100 - 25π .
The area of the red part in the diagram is therefore = area square – 2 x area not dotted
= 100 – 2(100 - 25π )
= 50π - 100.
The red part of Dan’s Badge is therefore 4(50π - 100) = 200π - 400 = 228.32 cm2.