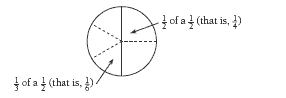Cutting It

This activity is about fractions and division into equal parts. These concepts are strongly related. To partition an area into fractions, the parts must be equal.
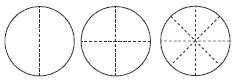
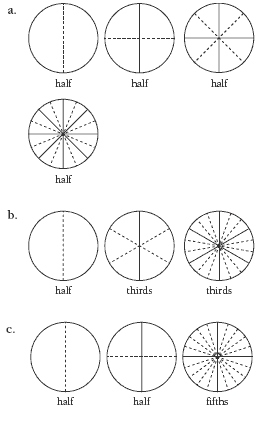
Spatially, some shapes are harder to partition than others. As long as a shape is regular and has reflective symmetry, it can usually be partitioned very easily into halves, quarters, eighths, and so on by folding:

Have your students use repeated halving to establish that halving halves gives quarters (fourths) and halving quarters gives eighths. This has a division equivalent: a number can be divided by 4 by halving and then halving again. (For example, 72 ÷ 4 =can be solved as 72 ÷ 2 ÷ 2 = 18.) Similarly, a number can be divided by 8 by halving three times in succession, because 2 x 2 x 2 = 8. (For example, 144 ÷ 8 =can be solved as 144 ÷ 2 ÷ 2 ÷ 2 = 18.)
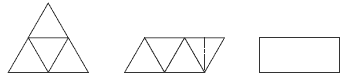
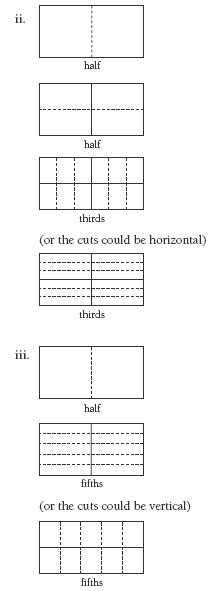
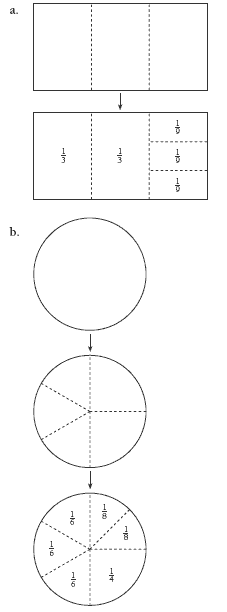
When doing question 1c, students are likely to find that a good first step is to exhaust any halving opportunities before moving on to thirding, fifthing, or whatever. So, to cut a pie into twelfths, they might proceed like this:

Finding twelfths by halving, halving, and then thirding (based on the fact that 2 x 2 x 3 = 12), has a division equivalent. For example, 264 ÷ 12 =can be solved using these steps: 264 ÷ 2 = 132, 132 ÷ 2 = 66, and 66 ÷ 3 = 22, so 264 ÷ 12 = 22.  Algebraically, if b = q x r x s, then a ÷ b = a ÷ q ÷ r ÷ s.
The learning point here is that many division problems can be solved more easily if they are done as a series of divisions by numbers that are factors of the divisor. For example, 972 ÷ 36 = 972 ÷ 2 ÷ 2 ÷ 3 ÷ 3 = 27 because 2 x 2 x 3 x 3 = 36.
It is also important that students understand that while partitioning can be thought of in terms of division, it can equally well be thought of in terms of multiplication by unit fractions (fractions with a numerator of 1). For example, the partitioning in question 1c ii (pictured as a rectangle above) can be represented mathematically as 1/2 x 1/2 x 1/3 = 1/12. Encourage your students to connect this with the fact that 2 x 2 x 3 = 12.
Some students struggle with the idea that multiplying by unit fractions (in fact, any fractions less than 1) gives them a result that is smaller than they started with. This is because they have generalised from whole numbers that multiplication “makes bigger”. One way of correcting this misconception is to refer students back to the whole-number view of multiplication that sees 3 x 4 =as “3 sets of 4”. It will then help if they can see 1/2 x 1/3 = as “one-half of one-third”. Another useful approach
is to use number patterns to help broaden the students’ ability to generalise, for example, the pattern  4 x 3 = 12, 2 x 3 = 6, 1 x 3 = 3, 1/2 x 3 = 1 1/2, 1/4 x 3 = 3/4, and so on.
Questions 3–6 involve unequal partitioning. Question 3 is designed to challenge the misconception that, if there are 5 parts, each part must be 1/5. It also leads on to an understanding that a whole (quiche) can be partitioned into 3 sixths and 2 quarters.
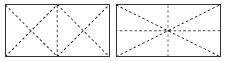
Students need to understand that when they partition a shape, area is conserved. That is, the sum of the areas of the parts equals the area of the whole. Discuss with your students how the triangle below is partitioned and the parts recombined to form a parallelogram that can then be partitioned to form a rectangle:

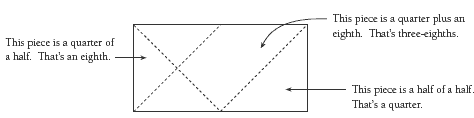
Question 4 requires the students to map parts back to the whole and to consider how many times a particular piece will fit in.
For example, for question 4d:

Taking the ideas further

Students could also use this activity to explore the idea that equivalent fractions can be created by splitting an existing fraction. To understand equivalent fractions, they need to hold the “1 whole” in their heads while considering the effect of splitting a fractional part. For example, if a part is defined as 1/3, then one-quarter of that part is 1/12 of the original whole (1).
This means that 1/3 is equivalent to of the same whole (that 1/3 = 4/12). Students should see that the numerator and denominator of have both been multiplied by 4 because there are now 4 times as many parts making 1/3 and 4 times as many parts making up the whole.

Answers to Activity

1. a. Mrs Cook halves, then halves, then halves again.
b. Drawings will vary. Two possible drawings are:

c. If Mrs Cook’s first cut is a half, then drawings should be similar to:

2.

3. Annie is right. The diagram below shows why.
 

4. a. Explanations may vary.

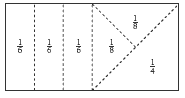
Half of the rectangle is divided into thirds. A third of 1/2 is 1/6. Half of the other 1/2 is 1/4, and 1/2 of 1/4 is 1/8.
b. Explanations may vary.

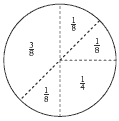
The right half is divided to give 1/2 of 1/2 a (that is, 1/4) and 2 lots of 1/2 of a 1/4, which is 2 lots of 1/8. The left half has one piece the same size as the 1/8 on the other side, so the bigger segment must be 3/8 because 1/8 + 2/8  = 3/8.
c. Explanations may vary.

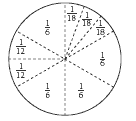
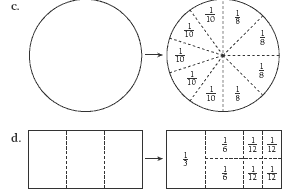
The circle is divided into sixths and fractions of sixths. (If you look to the right of one of the centre lines, you can see 3/6 in that half.) The top right parts are 1/3 of 1/6, that’s 1/18. The centre left parts are 1/2 of 1/6, that’s 1/12.
d. Explanations may vary.

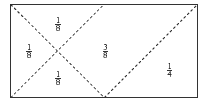
The bottom right-corner fraction is 1/2 of a 1/2, or 1/4. From there, you can work out that there are three 1/8 fractions, which means the last fraction must be 3/8 (1/4 + 1/8 + 1/8 +1/8 = 5/8; 5/8 + 3/8 = 1).

5. Drawings will vary, depending on where you put your dividing lines. Possible drawings include:

 

1

6. Problems will vary.