Solve multiplication and division problems by using proportional adjustment.
Number Framework Stage 7
Masking cards
Using Equipment
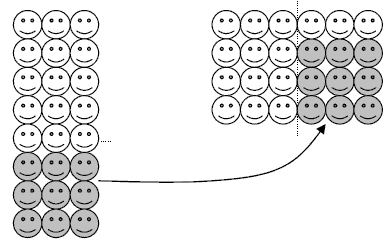
Provide each student and yourself with a Happy Hundred array and two masking cards. Show how eight threes could be shown using the masking cards.
Ask students to work out how many faces there are altogether.Discuss their strategies. Focus particularly on partitioning, forexample, “five threes and three threes.”
Ask the students to use the cards to block the rest of the faces so that “only eightthrees are showing.” Meanwhile mask your array to show four sixes. Ask them towork out how many faces your array has in total.
Note that 8 × 3 has the same total as 4 × 6. Ask students why they think this is true.Explain this by partitioning one of the arrays. Move the parts as shown (cut and paste).
4 × 6 = 24 = 8 × 3 = 24
Students may notice that each set of factors can be turned into the other by doubling and halving. Provide similar examples for modelling with the arrays. These might include:
4 × 5 = 20
2 × 8 = 16
2 × 6 = 12
4 × 10 = 40
2 × 10 = 20
4 × 4 = 16
4 × 3 = 12
8 × 5 = 40
Using Imaging
Predicting and Generalising: Ask students to imagine 3 × 16 on the smiley face sheet. Get them to describe the array. Write the expression 3 × 16 on the whiteboard.
Ask, “Which factor do you think could be halved? (sixteen) What is half of sixteen? (eight) How many eights will be in the array? (six) What will be the total number of faces? (forty-eight)”
Record the result as an equation: 3 × 16 = 6 × 8 Pose other problems that can be imaged and solved using doubling and halving. Examples might be:
5 × 18 = 10 × 9 3 × 12 = 6 × 6 14 × 4 = 7 × 8 24 × 5 = 12 × 10
Note, “Doubling and halving is like multiplying one factor by two and dividing the other factor by two. Will this work if you multiply and divide by three?”
Put up the expression 3 × 3. Ask, Will this still total nine if I multiply and divide by three? Students should note that this transforms 3 × 3 into 1 × 9 or 9 × 1. So trebling and thirding appears to work.
Problem: Can you use trebling and thirding to solve 27 × 3?
Support students with scaffolding questions like: Which factor would it make sense to divide by three? (twenty-seven) How many nines will be in the whole array? How do you know?
Pose related examples as given below. Ask students to use either doubling and halving or thirding and trebling.
2 × 18 = 4 × 9 = 6 × 6
24 × 3 = 12 × 6 = 8 × 9
Ask them to solve 2 × 36 by multiplying and dividing by four to see if that works as well (2 × 36 = 8 × 9).
Using Number Properties
Pose multiplication problems with larger numbers that are easy to calculate using doubling and halving, trebling and thirding, etc., strategies. Larger numbers are hard to visualise so this will promote generalisation of the number properties. Examples might be:
6 482 × 5 = 3 241 × 10 = 32 410
3 × 18 = 9 × 6 = 54
4 × 75 = 12 × 25 or 2 × 150 = 300
86 × 50 = 43 × 100 = 4 300
Independent Activity
Students should play the game of Metamorphosis (Material Masters 6-7) to consolidate the idea of doubling and halving, trebling and thirding, etc.