This is a level 3 algebra activity from the Figure It Out series. It relates to Stage 6 of the Number Framework.
Click on the image to enlarge it. Click again to close. Download PDF (283 KB)
find a relationship in a number pattern
Number Framework Links
Use this activity to:
• encourage transition from early additive strategies (stage 5) to advanced additive strategies (stage 6) in the domains of addition and subtraction and multiplication and division
• help the students who are beginning to use advanced additive strategies (stage 6) to become confident at this stage in the domain of addition and subtraction.
FIO, Levels 2-3, Number Sense and Algebraic Thinking, Book Two, Curling, pages 18-19
Copymaster of the Scorecard
This unusual context is an opportunity to link mathematics with a unique aspect of life in New Zealand. The problems involved will challenge your students to find and describe number patterns. They will need to develop a systematic approach to recording the relationships involved in setting up a tournament draw.
Introduce the activity using a New Zealand map to identify the towns in the Central Otago region where curling is popular. Information and photographs of outdoor curling can be found at http://www.curling.org.nz/index.php/clubs-&-competitions/schools
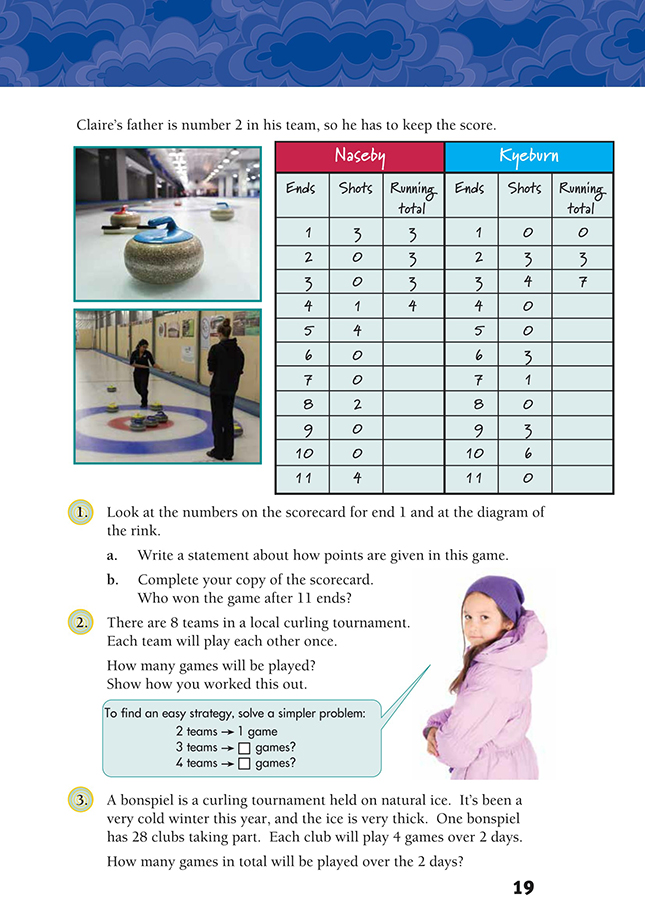
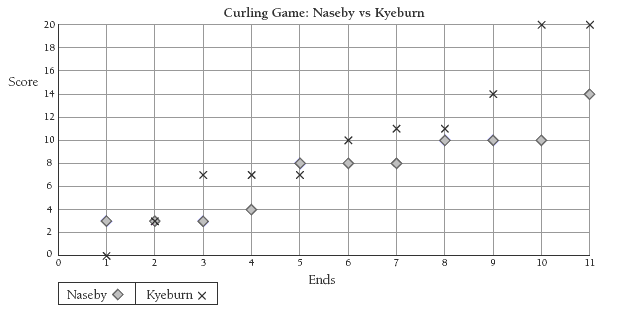
Question 1 consolidates students’ understanding of the game of curling and presents an opportunity for building basic addition strategies using the running total column of the scorecard. The scorecard is a great context for developing the understanding and use of relationship graphs. Model the necessary axes and labels and have the students complete the graph. For example:
As an extension to this question, the students could develop a tabletop version of curling, using counters as stones and delivering the stone with a flick of their finger, aiming at a 5 cent coin as the pot lid. They could then practise graphing their scorecards as relationship graphs.
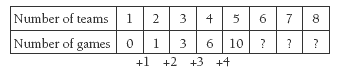
To solve question 2, the students explore a real-life application of algebra skills. The use of a table showing the results of the “solve a simpler problem” strategy illustrated in the text will help the students to find a pattern and use it to solve the problem.
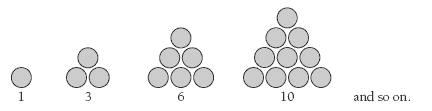
The students may recognise the pattern in the number of games table as the triangular number pattern that occurs in many other problems, such as the handshake problem (the pattern generated when asking for the number of handshakes done by pairs of people in any sized group). You can generate the triangular numbers pattern by forming triangles with counters:
You may need to suggest some ways for the students to work out the number of games played inquestions 2 and 3. One way is to use network diagrams.
Model the round-robin table structure (shown in the Answers) and help your students’ understanding with questions such as:
How many squares are inside the 8 by 8 table?
How many squares can show 2 different teams against each other? (64 – 8 = 56)
Point out that this is 1 fewer 8 than the 8 by 8 of the whole square, so it is 7 x 8 = 56. Each game is repeated on the table, so how many actual games are there in total? (56 ÷ 2 = 28).
Extension
Re-explain the use of the round-robin table to solve the problem: Let’s see what’s happened from the start. We had 8 x 8, which became 8 x 7. Then we divided by 2, so we have of 8 x 7 = 28. Have students make a round-robin table to work out the total number of games with 2, 4, 5, 6, and 10 teams. Ask them to record the games for each number of teams in one equation:
2 teams: (2 x 1) = 1
4 teams: (4 x 3) = 6
5 teams: (5 x 4) = 10
6 teams: (6 x 5) = 15
10 teams: (10 x 9) = 45
Ask the students to describe the pattern in these equations. They may see that they always find a half of the number of teams multiplied by 1 fewer than the number of teams. For question 3, check that the students realise that each team is restricted to 4 games so this tournament is not a round-robin. (See the comment in the Answers.)
Answers to Activity
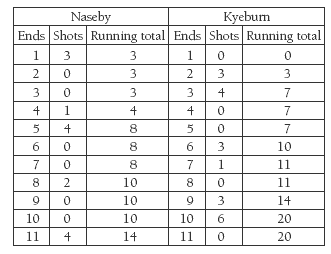
1. a. Statements may vary. The team whose stone is closest to the pot lid gets a point for that stone and for any other of their stones within the circles that are closer than the nearest opposition stone. (For example, Naseby won the first end with 3 shots.
Kyeburn had 1 stone inside the outer circle, but it wasn’t counted. Only one team scores from an end.)
b. Kyeburn won, with 20 points. Your scorecard should look like this:
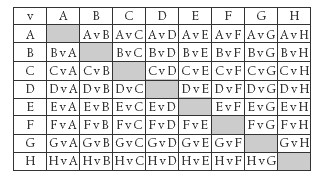
2. 28 games. Strategies will vary. For example, you could make a table, look for a pattern, act it out, or draw a diagram. A round-robin table for 8 teams would look like this:
Note that all the games on the left side of the centre diagonal are repeats. For example, A v B is the same game as B v A.
3. 56 games. (28 x 4 ÷ 2. You have to divide by 2 because 2 teams are involved in each game.)