These are level 3 number, and geometry problems from the Figure It Out series.
A PDF of the student activity is included.
Click on the image to enlarge it. Click again to close. Download PDF (333 KB)
use addition and multiplication to solve problems (Problems 1 and 4)
explore different two dimensional shapes (Problem 2)
explore reflections with paper folding (Problem 3)
Problem One
This question is very similar to Problem One, page 2.
A good strategy is to use a table with trial and improvement. In the table, the number of letters and cards is always 16.
The first row is a guess, and the second row shows the change in cost if you add on one letter. An extra letter costs an extra 15 cents. The first guess totalled $5.55, and you know that Irene spent $5.40. You can reduce the cost by 15 cents if Irene sent one fewer letter and one more card than in the first guess. So Irene sent four letters and 12 cards.
Problem Two
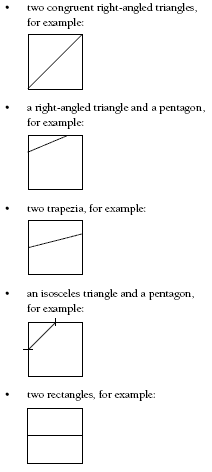
a. Students could experiment with different cuts and then come together as a class or group to compare their different cuts. Students who are working systematically will probably have tried all the cuts from one corner, then all the cuts from another corner, and so on, and then all the cuts from one side, all the cuts from another side, and so on. You may need to point out to them that all the cuts from the other corners will just give reflections or rotations of the cuts from the first corner. The same applies for the sides: all the cuts from the last three sides are reflections or rotations of cuts from the first side. So there are only two places the cuts can start from: a corner (it doesn’t matter which) or a side (it doesn’t matter which).
From a corner, you can either go to an opposite side (it doesn’t matter which – a cut to one side will be a reflection of a cut to another side) to get a right-angled triangle and a trapezium
or to the opposite corner to get two right-angled, isosceles triangles:
From a side, you can either go to an adjacent side to get a right-angled triangle (that may be isosceles) and a pentagon:
or to the opposite side to get two trapezia or two rectangles:
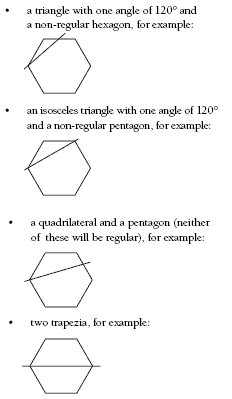
b. With a hexagon there are more possibilities, so you have to be a bit more careful. However, you can still only start a cut from a corner or a side. As a result, you get:
• a cut through a corner
i. a triangle with one angle of 120° and a non-regular hexagon;
ii. an isosceles triangle with one angle of 120° and a non-regular pentagon;
iii. a quadrilateral and a pentagon (neither of which can be regular);
iv. two trapezia.
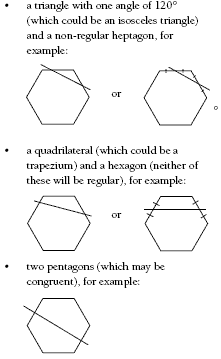
• a cut through a side
i. a triangle with one angle of 120o (which may or may not be isosceles) and
a non-regular heptagon;
ii. a quadrilateral (which may be a trapezium) and a hexagon (neither of which can
be regular);
iii. two pentagons (which may be congruent).
These diagrams are provided in the Answers.
Problem Three
Most students will find this hard to visualise. Start by asking them to visualise the paper with one fold. Ask them how many creases there are.
If they visualise folding it again, they would be putting a crease into each of the two previously unfolded sections. So there are now three creases (the original crease plus the two new ones). The strip is now in four sections.
The third fold puts a crease in each of the four previously unfolded pieces. So now there are seven creases.
The students can then check by folding a strip of paper.
Problem Four
One bowl of rice is served for two guests, one bowl of soup for three guests, and one bowl of meat for four guests, so the number of guests must be divisible by 2, 3, and 4. 2 goes into 4, so you only have to find numbers that are divisible by 3 and 4. These could be 12, 24, 36, 48, … or in fact any multiple of 12.
Now check how many bowls of rice, soup, and meat these numbers would give and stop when you find that you are using 39 bowls.
For 12 guests, you would need six bowls of rice, four bowls of soup, and three bowls of meat. This gives 13 bowls, which is not enough. But 13 x 3 = 39, the number of bowls used at the banquet, so you need three times as many bowls and also three times as many guests. 3 x 12 = 36, so there are 36 people.
Hints for Students
1. You could use trial and improvement and record your results on a table.
2. Try using equipment or drawing a diagram. Work systematically and experiment with making cuts from different parts of the square. Use a similar method for the hexagon.
3. Think. Try to visualise the problem. Fold a strip of paper or try a smaller case first if you are having difficulty.
4. Try a smaller case first (for example, if just rice and soup were served). Can you find a pattern that will help you work out the larger problem?
Answers to Problems
1. Four letters and 12 cards
2. a. You can also get:
b. By cutting through a corner, you can get:
By making a cut through a side, you can get:
3. 7 creases
4. 36 guests