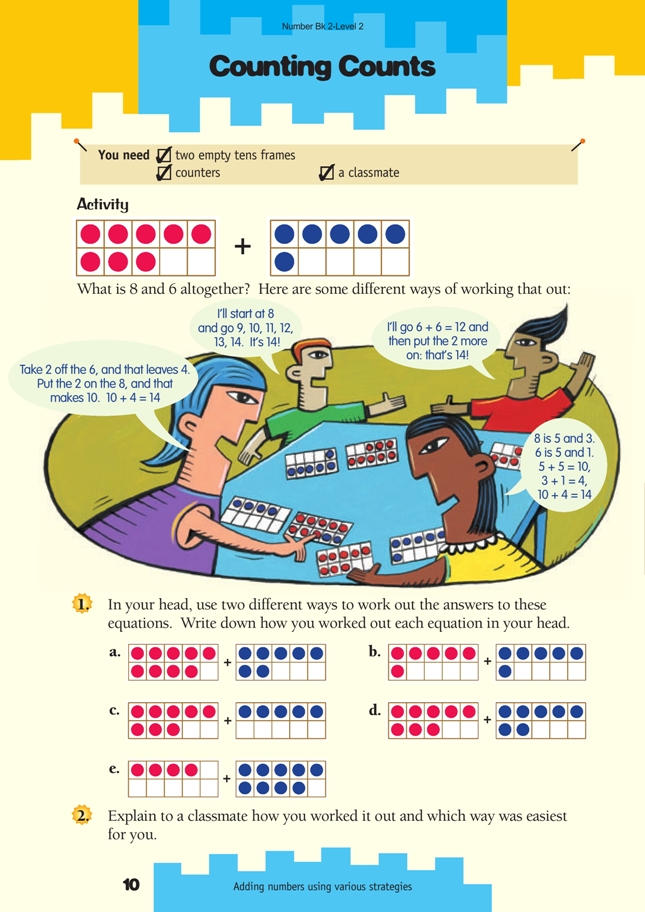
This is a level 2 number activity from the Figure It Out series. It relates to Stage 5 of the Number Framework.
A PDF of the student activity is included.
Click on the image to enlarge it. Click again to close. Download PDF (211 KB)
use tens frames to explore different mental strategies for addition
- FIO, Level 2, Number, Book 2, Counting Counts, page 10
- Two empty Tens Frames
- Counters
- Classmate
This activity is designed to move students on from counting strategies to part-whole strategies. Of the four possible strategies shown on the page, three are part-whole and one is counting.
The important prior knowledge that students need to use a part-whole strategy is:
• doubles up to 20, for example, 6 + 6 = 12
• addition facts that make 10, for example, 9 + 1 = 10
• addition facts that are 10 and more, for example, 10 + 6 = 16.
Representing the numbers on tens frames is critical for the students to be able to develop their own mental images of how the numbers are being partitioned and regrouped.
If your students are having difficulty with the concept of regrouping, get them to physically move counters around on tens frames. For example, for 8 + 6, have eight blue counters on one tens frame and six red counters on another tens frame. Ask the students to make a ten by moving two red counters from the 6 to the 8. This clearly shows the regrouping and confirms that no counters have been added or removed; they have simply been regrouped. Now 10 are on one frame and 4 are on the other, and the students will know the answer to this as a basic fact (10 + 4 = 14). It’s very
important that the students see the benefit in the regrouping and can see this strategy as a faster, easier, and more efficient way to add numbers together.
In this activity, the students initially need to be able to choose their own recording methods for question 1. For example, some students will represent their strategies graphically, possibly by drawing the tens frames and circling parts or by using arrows. Then through discussion, sharing, and teacher modelling, they can gradually refine their recording to a simple numerical representation.
The students’ discussion in question 2 about which strategy they chose and why they found it easy is important for when they deal with larger numbers later on. For example, 6 + 6 encourages using doubles facts rather than making a 10: (6 + 4) + 2. Later on, problems such as 25 + 26 would most easily be solved by using doubles: (25 + 25) + 1 rather than making a 10: (25 + 5) + 21. Ultimately, the students should have a range of strategies they can choose from to solve problems in the most efficient way possible.
As an extension, you could pose problems such as 28 + 6 or 47 + 7 to see if the students can transfer the strategy beyond 20.
Answers to Activity
1. a. 16. Examples of methods are:
(9 + 1) + 6 = 16
(5 + 5) + (4 + 2) = 16
(7 + 7) + 2 = 16
9 ... 10, 11, 12, 13, 14, 15, 16
b. 12. Examples of methods are:
(6 + 4) + 2 = 12
(5 + 5) + (1 + 1) = 12
6 + 6 = 12
6 ... 7, 8, 9, 10, 11, 12
c. 13. Examples of methods are:
(8 + 2) + 3 = 13
(5 + 5) + 3 = 13
8 ... 9, 10, 11, 12, 13
d. 15. Examples of methods are:
(8 + 2) + 5 = 15
(5 + 5) + (3 + 2) = 15
(7 + 7) + 1 = 15
8 ... 9, 10, 11, 12, 13, 14, 15
e. 13. Examples of methods are:
(9 + 1) + 3 = 13
5 + (4 + 4) = 13
(4 + 4 + 4) + 1 = 13
9 ... 10, 11, 12, 13
2. Answers will vary.