This is a level 3 geometry activity from the Figure it Out series.
A PDF of the student activity is included.
Click on the image to enlarge it. Click again to close. Download PDF (327 KB)
identify diagonals in two dimensional shapes
FIO, Level 3-4, Geometry, Cornered!, page 1
ruler
Activity One
This activity is useful for reinforcing students’ understanding of the geometric terms vertex (plural: vertices) and diagonal. A vertex is the corner point of a polygon or polyhedron. It is also the point where two or more rays or line segments meet. A diagonal is a line segment that joins two vertices of a polygon but is not a side.
The students are asked in question 2 to find shapes with two diagonals. They can experiment with different shapes and should realise that all quadrilaterals have two diagonals.
.gif)
Activity Two
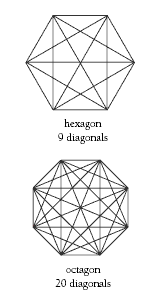
A systematic way of recording the diagonals for the octagon in question 2 is:
AC AD AE AF AG
BD BE BF BG BH
CE CF CG CH
DF DG DH
EG EH
FH
Finding the diagonals of regular shapes can lead students to create patterns such as the star patterns created by the regular pentagon and hexagon.
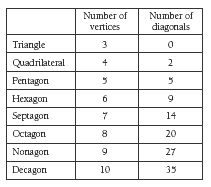
In question 3, the students examine their tables for patterns. One pattern is described in the Answers, but there is a rule for this that you may like to explore with the students. For example, the octagon has eight vertices. Five diagonals can be drawn from each vertex. This would seem to give a total of 40 diagonals, but 20 of these have already been drawn from other vertices, so there are only 20 diagonals (40 ÷ 2). (Another way to look at it is that each diagonal has been counted from both ends.)
There is a general rule that you can use to calculate the number of diagonals a polygon has. First, you need to find out how many diagonals radiate from any one vertex of the polygon.
1. Each diagonal connects two vertices. So, start by dividing the number of vertices by 2.
(In the case of the octagon, 8 ÷ 2 = 4.)
2. Multiply your answer from step 1 by the number of vertices – 3.
(For the octagon, 4 x (8 – 3) = 4 x 5 = 20.)
Why subtract 3?
Firstly, when you join a vertex of a polygon to every other vertex in the polygon (that includes the two adjacent vertices), you will always have one line less than there are sides to the polygon. Check this!
Secondly, the lines joining adjacent vertices are not diagonals. There are two of these lines to every vertex. So the number of diagonals radiating out from any vertex is the number of sides that the polygon has – 1 – 2, which equals n – 3.
As an algebraic formula, this rule is 1/2n x (n – 3) where n is the number of vertices the polygon has.
Students who are comfortable with algebraic notation could try out this rule on the shapes in their chart. (This activity connects to the Algebra strand.) See also Problem Four, page 11, in Problem Solving, Figure It Out, Levels 3–4.
Answers to Activity
Activity One
1. Answers will vary, but the shapes can be any shape with four vertices. For example:
2. Shapes with four vertices (four-sided polygons)
3. Two. (A diagonal does not have to be within the shape.)
Activity Two
1. Yes, C to E
2.
3. a.
b. The difference between each number of diagonals increases by 1 for each extra vertex (+ 2, + 3, + 4, + 5, and so on).