The purpose of this activity is to support students in comparing ratios that do not have a common part or whole. They do so by using their knowledge of fractions, and by expressing the part-whole relationships as fractions.
- Connecting cubes
- Calculators
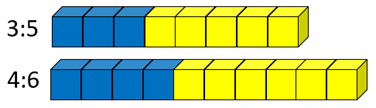
Pose the following problem, using cube models.
Which ratio has the stronger taste of blueberry? How do you know?
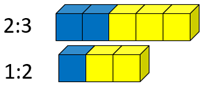
Look for students to consider the relationships between parts and wholes when making their decision. Watch for attention to a single part, e.g. “2:3 is stronger because it has more blueberry.”
Some students may reproduce copies of the ratios until a common part or whole is found. For example, doubling 1:2 gives 2:4 which has a common number of blueberry parts as 2:3.Ask students to create a ratio table for the comparison and record the part whole fractions.

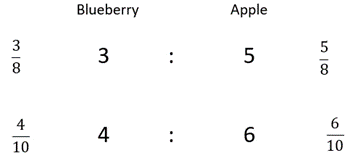
In this case students should know which fraction, 2/5 or 1/3, is greater. If they do not know, then explore the intervention on fractions as numbers at another time. Using a calculator is one way to compare the fractions.
2/5 = 2 ÷ 5 = 0.4 and 1/3 = 1 ÷ 3 = 0.33.
Ask students to record the inequality 2/5 > 1/3 and make a statement about the ratios. For example: “2:3 has a stronger blueberry taste because it is 2/5 blueberry. 1:2 is only 1/3 blueberry.”- Pose further problems using the same process for comparison. The difficulty of comparison is related to the nature of the part-whole fractions involved. Choosing ratios that make it difficult to copy ratios and find a common part or whole encourages students to use the fraction relationships. Use the calculator where necessary to confirm students’ ideas about the size of the fractions. Ask students to write a convincing argument about which ratio tastes more strongly of blueberry.
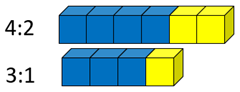
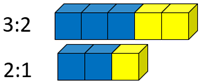
Good examples are shown below:
- Which ratio has the stronger taste of blueberry? How do you know?


Next steps
- Increase the level of abstraction by progressing from using cube models, to diagrams, and then to symbols only. Progress to word problems that require students to create the ratio model themselves. For example:
Lucy experiments with mixtures of mango and orange juice. She tries two recipes:
5 litres of mango juice with 4 litres of orange juice
3 litres of mango juice with 2 litres of orange juice
Which recipe will have the strongest orange flavour.
- Vary the context in which the ratios are presented. The context might include mixing paint, the amount of two elements on a plate, making cement, or creating a metal alloy. Consider which contexts can enhance links to your students' cultural backgrounds, interests, and learning from other curriculum areas. For example:
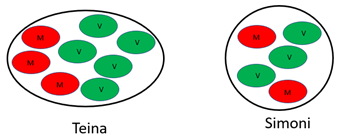
Teina and Simoni enter Masterchef Junior. They present their first plate with these ratios of meat to vegetables.
Whose plate has the biggest fraction of meat?