Comparing boxes by volume

Note: Volume is the measure of space taken up by a three-dimensional object. The space within a container is known as its capacity. As the thickness of many containers is negligible, it has become acceptable to refer to the space inside as volume too. You might frame the purpose for finding capacity within a context that is relevant to your students' interests, cultural backgrounds, and to learning from other curriculum areas. The māori kupu for volume is rōrahi.

1. Show the students the grocery packets A and B that are cut to different heights. 
   Which packet will hold the most rice? How do you know?
   Students should comment that one box is taller than the other. Some may note that the packets are the same length and width.
   Confirm the relative volumes by filling one packet with rice and then pouring the rice into the other packet. 
    
2. Take packet B away and replace it with packet C.
   Does packet C hold more rice than packet A? How do you know?
   Once students have decided which packet holds more, check the comparison by filling and pouring rice. See if students can use transitive reasoning.
   E.g. Packet A holds more than packet B and packet C holds more than packet A.
    
3. Together, decide on a method for recording these comparisons. This might use symbols (e.g. A > B and C > A), physical materials to construct a continuum, and/or verbal expressions (e.g. we know packet A is bigger than packet B because...). Consider what means of action and expression will be most appropriate for your students, and for the amount of cognitive load this task presents to them. You might also group students, encouraging tuakana-teina, and have the groups record their thinking in a variety of different ways.
    
4. Provide time for students to share their recorded comparisons.
    
5. Present students with packets B and C.
   Which packet holds the most, C or B?
   Students should recognise that C holds more rice than B without comparing the packets.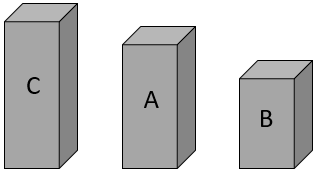
   
    
6. Follow the same process with packets, P, Q and R. Compare the packets two at a time. 
   Which packet holds more rice, Q or R? How do you know?
   Look for students to recognise that comparing the volume of cuboids that are the same height can be done using the area of the cross-sections.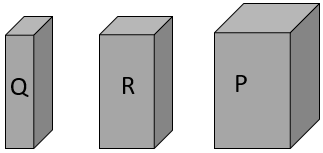
   

7. Progress to comparing packets X, Y, and Z. Ask students to predict which packet holds more and defend their position with a partner.
   Which packet holds more rice, X or Y? How do you know?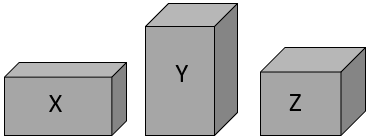
    

   After the predictions, fill one packet with rice and pour the contents into the other packet.
   What does this tell us about the volume of packets X and Y?

   • Does Y hold more because it is taller?
   • Does X hold more because it is wider?
   • Can a packet be moved to make it easier to see which one holds more?
      
8. Compare another two packets, say Y and Z. Focus students’ attention on both height and cross-section area. I n this example, Y is taller than Z but has less cross-sectional area.
   What can we say about the height of Y and Z?
   What can we say about the base area of Y and Z?
   How can we use what we know to predict which packet holds more rice?
    
9. Look for some students to compensate between height and base area. For example:
   I think Z holds more because it is a lot wider but not much shorter than Y.
   I think if you cut Y in half like this (horizontal) you could make a box the same height as Z but with more width.
   After students predict the result, pour rice between the packets to check the volume comparison.
    
10. Finally, encourage students to use logic to order the three packets by volume. In some cases, another pair comparison may be needed. For example, If X > Y and Z > Y then X and Z will need to be compared.
    Give the students pictures of two packets at a time. Ask them to predict which packet holds the most rice and defend their position to a partner, and then express their reasoning using words, symbols, and/or direct comparison and drawing.
                                           

Next steps 

1. Give students open-ended challenges involving area like this:
   • Draw three packets that look different but hold the same amount of rice.
   • Draw three packets that look the same but hold different amounts of rice.
2. Investigate volume in real life. Look at packaging of supermarket items or the volume of items in the classroom (e.g. books, desks, pencil cases). For example, you might look at cereal boxes.
   Which packet of cornflakes holds the most? How do you know?
   Open the packets and look at the contents.
   Why might makers of cornflakes create packets like that?