This problem solving activity has a geometry focus.
Fred was a man who laid tiles.
He had this beautiful big 1 metre by 1 metre square tile for part of Sue’s new kitchen floor.
But he broke it as he was putting it down.
Fred couldn’t replace the tile but he did find four square tiles to fill the space of the big one.
He laid three of these tiles perfectly but as he was putting the last one in place he broke it.
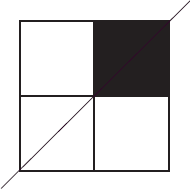
So at this stage, Sue had three tiles that formed a pattern with an axis of symmetry through the diagonal of the larger square.
In fact it looked like this:
It has reflection symmetry about the line through the diagonal.
Fred couldn’t replace these new smaller tiles, so, in the hole where the broken one should have gone, he started to lay four even smaller tiles.
He laid three of these tiles perfectly but as he was putting the last one in place he broke it.
In how many ways could he have laid these tiles so that the floor had reflection symmetry?
Fred couldn’t replace these new even smaller tiles, so, in the hole where the broken one should have gone, he laid four smaller again tiles.
He laid three of these tiles perfectly but as he was putting the last one in place he broke it.
In how many ways could he have laid these tiles so that the floor had reflection symmetry?
- Recognise and invent patterns with reflection symmetry.
- Devise and use problem solving strategies to explore situations mathematically (make a drawing, use equipment).
This problem is one of three parallel problems. Each one takes up the basic theme of Fred and his difficulty with tiles. This one focuses on geometric understanding, while the other two focus on statistical and numerical aspects (see The Clumsy Tiler C and The Clumsy Tiler B, respectively). All of the problems are at Level 4.
One of the key points in these lessons is to show that by changing a problem by just a little, it ends up in another strand of the curriculum.
The current problem deals with the different ways that tiles can be laid and have reflection symmetry. The extension takes in rotational symmetry. Symmetry plays an important role in mathematics. Because symmetric things are clearly related, an argument that applies to one will apply to another. For instance, suppose we were thinking about all the ways that there are of playing Noughts and Crosses. If we start with a cross, then there are only essentially three places that we need to worry about putting it. This is because the all the corner squares are the same and all the middle squares on a side are the same too.
On the other hand in a more geometrical setting, if two things are symmetric and we know the dimensions of one of them, then we know the dimensions of the other. This type of argument is at the root of trigonometry. Not only does trigonometry allow us to find heights of mountains, a geometric application, but it also allows us to predict all manner of things that behave in a periodic way that may have nothing to do with geometry at all.
- Copymaster of the problem (English)
- Copymaster of the problem (Māori)
- Square pieces of cardboard
Problem
Fred was a man who laid tiles. He had this beautiful big 1 metre by 1 metre square tile for part of Sue’s new kitchen floor. But he broke it as he was putting it down.
Fred couldn’t replace the tile but he did find four square tiles to fill the space of the big one. He laid three of these tiles perfectly but as he was putting the last one in place he broke it. So at this stage, Sue had three tiles that formed a pattern with an axis of symmetry through the diagonal of the larger square. In fact it looked like this:
It has reflection symmetry about the line through the diagonal.
Fred couldn’t replace these new smaller tiles, so, in the hole where the broken one should have gone, he started to lay four even smaller tiles. He laid three of these tiles perfectly but as he was putting the last one in place he broke it. In how many ways could he have laid these tiles so that the floor had reflection symmetry?
Fred couldn’t replace these new even smaller tiles, so, in the hole where the broken one should have gone, he laid four smaller again tiles. He laid three of these tiles perfectly but as he was putting the last one in place he broke it. In how many ways could he have laid these tiles so that the floor had reflection symmetry?
Teaching Sequence
- Discuss floor tiles and have students identify places they know are tiled. Ask:
How do they lay tiles like that? - Tell them about Fred.
What did his first tile look like?
What did the second one look like? How big was it? - Pose the problem. Have students work in groups or pairs to solve it. Encourage them to keep a clear record of their process.
- Have groups that finish quickly work on the extension problem.
- Ask one or two of the groups to tell how they solved the problem. Provide an opportunity for others to question if they don't understand. Some of the students who worked on the Extension problem might like to report back too.
Solution
There are four possible positions for the hole (see image below). The first two are on the diagonal axis of symmetry, and the whole design remains symmetrical. The third and fourth designs are not symmetrical.
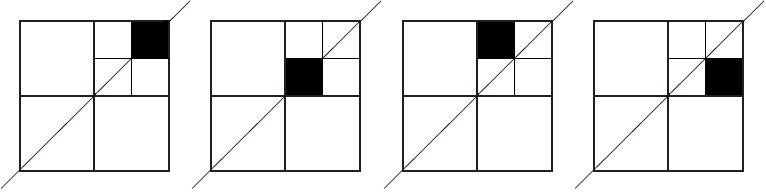
Regardless of which of the two symmetrical layouts he uses, there are four possible positions for the missing "even smaller tile". Two of those will are on the axis of symmetry and the design will remain symmetrical.