Close Ties

This activity is designed to encourage students to acquire number sense about the relative size of fractions. 0, 1/2, and 1 are used as benchmarks, and they are very useful for estimation problems with fractions where only approximate answers are required. To have a strong understanding about the size of fractions, the students need to consider the multiplicative relationship between the numerator (top number) and denominator (bottom number) of the fraction. Some students assume that fractions can only be numbers that are less than 1. You may need to introduce or
revise the idea of “improper fractions”, for example, 13/4 = 3 1/4, where the fraction describes 1 single whole.
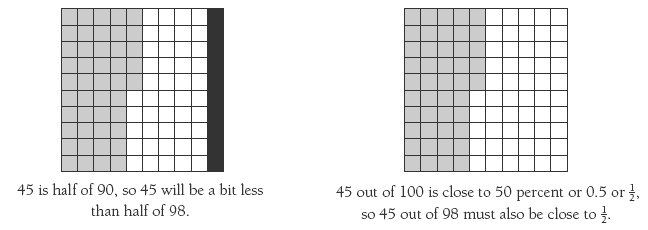
Question 1a asks the students to consider whether 45/98 is closer to 0, 1/2, or 1. The denominator suggests that 1 has been cut into ninety-eighths, that is, 98 equal parts. Students who are having difficulty could work through the problem using a hundredths grid.

Kimiora’s speech bubble reflects an additive comparison of the denominator and numerator. This “gap” thinking is common among additive thinkers and can be challenged by counter example. Start with fractions that have small denominators that the students may already know. Test the theory that a large gap between the numerator and denominator means that the fraction is small and therefore, a small gap means that the fraction is large. Consider 1/2, 2/3, 3/4, and 4/5. They all have
the same gap of 1 but get progressively larger and closer to 1.

Try other fraction combinations that have as large a gap between the numerator and denominator as 45/98. For example, 147/200 and then 447/500. The students could make wafer bars with 200 and 500 little squares in them and shade in 147 and 447 of them. The Table function in a word processing program is good for this because you can create a 1-cell table that is full page size and then use the Split Cells function to divide it into as many parts as you want. You can then do shading in blocks. This way, the size of 1 stays constant. The students will soon find that about 3/4 of the 200 square wafer and about 7/8 of the 500 square wafer is shaded. After this, the students should accept that nearly half of the squares in the hundredths grid for the 45/98 problem will be shaded.
In question 1b, the size of the numerator and denominator are deliberately pushed up to encourage the use of number properties. The students won’t have ready access to physical models to decide whether 999/10 000 is closer to 0, 1/2, or 1. Questions that might be used to scaffold student thinking could be:
What tidy number is 999 very close to? (1 000)
About how many times will 999 go into 10 000? (10)
Do you know any other fractions where the denominator is 10 times as big as the numerator? How big are those fractions? (222/2220, 333/3330, and so on. Each fraction is 1/10.)
So for question 1b, note that only one of the speech bubbles (Kimiora’s) shows correct reasoning (although Ruth makes a good start). A student who agrees with either of the first two speech bubbles is probably still thinking that the size of a fraction is determined by the size of either the numerator or the denominator.
It’s not really a good idea to let the students use a calculator to confirm the proximity of a fraction to 0, 1/2, or 1. Using a calculator not only undermines the development of sound number sense, it also, at the same time, makes assumptions about the relationship between the division operation and fractions and decimals
In questions 4 and 5, the students need to make deductions about the sum of two fractions based on their understanding of fraction size. Students who have a good understanding of equivalent fractions will know that 8/16 equals 1/2, so 7/16 is less than 1/2. This means that, in question 4, 7/16 + 1/2 must be less than 1.
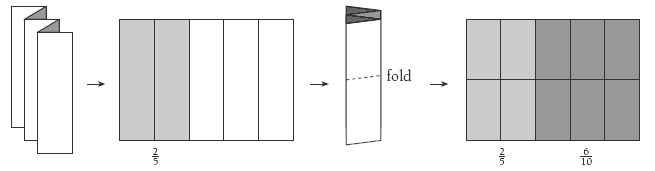
Question 5 is more difficult because it involves the size of two fractions, one more than 1/2 (that is, 6/10) and one less than 1/2(that is, 2/5). Again, the students need to use equivalent fractions. A piece of paper can be used as a model. The students can fold the paper into 5 equal parts and then shade in 2/5 (2 fold sections). If they then fold the paper once, lengthwise, which gives tenths, and shade 6/10, they will see that the whole piece of paper is shaded, showing that 2/5 + 6/10 = 1.

Extension

Extend the students by posing more difficult problems that require them to apply benchmarks such as 0, 1/2, 1, 1 1/2, and so on. Good examples are:
7/12 + 6/13: Is the answer smaller than, equal to, or larger than 1?
9/10 –  3/8: Is the answer smaller than, equal to, or larger than 1/2?
99/100 + 100/101: Is the answer smaller than, equal to, or larger than 2?
 

Answers to Activity

1. a. Alice and Ruth are both right. Kimiora is wrong. The size of a fraction is based on both the numerator (top number) and the denominator (bottom number). The
difference between these numbers by itself will not give the size of the fraction.
b. Alice is wrong. 999 is a large number, but as a numerator, it’s small in relation to the denominator, 10 000. 999 is nearly 1/10 of 10 000, so the fraction is close to 1/10.
Ruth is right, but it’s not just the big number on the bottom that makes the fraction small. For example, 9 999/10 000 has 10 000 on the bottom but is very close to 1.
Kimiora is right. 5/10 is 1/2, so 1/10 must be closer to 0.
2. Answers will vary. You can’t tell if a fraction is close to 0, 1/2, or 1 simply by looking at the numerator or the denominator. You need to look at the size of the numerator compared with the denominator. If necessary, you can round one
or both of the numbers to make this easier. If the numerator is about half of the denominator, the fraction is closer to 1/2, if it is a lot less than the denominator, it is closer to 0, and if it is nearly as big as the denominator, it is closer to 1. Ask:
“What do you multiply the numerator by to get the denominator?”
3. a. Closer to 1
b. Closer to 1/2
c. Closer to 0
d. Closer to 1. (It’s actually bigger than 1.)
4. You are right if you agree with Ruth’s and Alice’s thinking. Both should be able to get the correct answer.
Ruth: 7/16 is smaller than 8/16, which is 1/2, so 1/2 + 7/16 < 1 (is less than 1).
Alice is right in changing 1/2 to 8/16 so she can add 8/16 + 7/16 = 15/16. 15/16 < 1
Kimiora is wrong. You don’t add the denominators, and the denominators have to be the same before you can add the numerators. You can’t add a fraction bigger than 1/18 (in this case, 7/16) to 1/2 and finish with an answer that is less than 1/2.
5. The answer is equal to 1. (2/5 + 6/10 = 4/10 + 6/10 = 10/10 = 1)

( + = +
=
= 1)