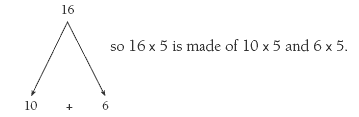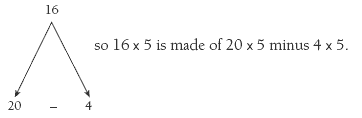This is a level 3 number activity from the Figure It Out series. It relates to Stage 6 of the Number Framework.
Click on the image to enlarge it. Click again to close. Download PDF (170 KB)
use multiplication facts and mental strategies to solve multiplication problems
Number Framework Links
Students using advanced counting (stage 4) strategies can solve these problems using materials and by skip counting, for example, in fives.
Use this activity to:
• help the students who are beginning to use early additive strategies (stage 5) to become confident at this stage in the operational domain of multiplication and division
• encourage transition from early additive strategies (stage 5) to advanced additive strategies (stage 6)
• help your students to consolidate their knowledge of basic facts.
FIO, Levels 2-3, Number Sense and Algebraic Thinking, Book One, Clean Cars, pages 18-19
A classmate
This activity allows students to use strategies ranging from advanced counting to early multiplicative thinking. If necessary, help the students to link their counting or addition strategies to multiplication as a more efficient form of thinking for this type of situation. (The three strategies depicted all use multiplication.)
For this activity, a recall of basic multiplication facts is desirable. Students without this knowledge need to be able to skip-count in at least 5s and 10s and be able to derive an unknown multiplication fact from a known fact or use a basic fact reference chart.
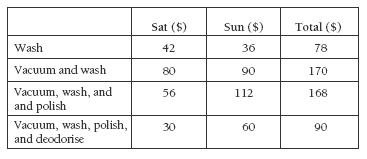
Introduce the activity to a guided teaching group by discussing the differences in the grooming types and charges. Have the students convert the tally chart into numbers to ensure that they understand it.
Question 1 is the key to meeting the achievement objectives for this activity. To find out what strategies your students already have, ask them to attempt to solve the question individually or in groups before looking at the strategies suggested in the speech bubbles. After they report back, they can compare their strategies with those suggested in the speech bubbles and then complete those statements.
The students who are already confident at stage 5 (early additive) or above could begin by discussing and completing the speech bubble strategies.
For some students, you may need to clarify some of the strategies. Place value materials, counters, or cubes will be important in modelling these strategies. For question 1a, ask the students: How has Sam made it easier to work out 16 lots of 5? The explanation should highlight the place value split:
For question 1b, repeat the question: How has Tanya made it easier to work out 16 lots of 5? The students may need a chart like this to help them see the strategy:
If necessary, use a bead frame to model this pattern.
As an algebraic extension, ask the students to find a generalisation that describes any number of 5s makes what number of 10? The generalisation can be expressed as: “The number of 10s is half the number of 5s” or “There are twice as many 5s as 10s.”
For question 1c, again ask: How has Ariana made it easier to work out 16 lots of 5? In response, the students should identify a subtractive split.
Have the students work in small groups to attempt questions 2–4. For the students who need to use materials, the bead frame would be an excellent tool to help them model the problem and for you to use as you re-explain some strategies.
For the students using imaging, Number Line in Tens (Material Master 5-12), would help them to image the actions used on the bead frame and provide a link to recording with numbers.
The reporting back and sharing of strategies from each group will be the time to clarify and compare strategies. As the students report back, it can be helpful if you record the strategies they used on the whiteboard, making sure that the recording accurately reflects the report.
Answers to Activity
1. Answers may vary. Possible ways to complete
and explain each strategy are:
a. “... I added 50 and 30 to get $80.” Sam’s strategy uses the fact that 10 + 6 = 16.
b. “... 8 tens or 80.” Tanya’s strategy uses the fact that 2 x 8 = 16.
c. “... 20 is 4 lots of 5. This gave me $80.” Ariana’s strategy uses the fact that
20 – 4 = 16.
2. a
Note: The “Total ($)” column is not asked for in the question, but it’s useful for question c.
b. Strategies will vary and include those shown in question 1. You could use your basic facts (8 x 7 = 56) for Saturday’s vacuum, wash, and polish and double that amount for Sunday. Or you might add 50 + 50 + 12 = 112. The simplest way to
find the total for the vacuum, wash, polish, and deodorise is to use your 10 times table.
c. $506
3. a. Vacuum and wash
b. Vacuum, wash, and polish
4. $44. (550 – 506)