Choosing units of length for greater precision

1. Set up a scenario where the object being measured has a length ‘between’ whole centimetres.

   I want to measure the length of this pencil as accurately as I can.
   What does accurately mean?
   Discuss the idea that if the measurement is precise enough, another person could locate the pencil you measured among a collection of them.
   How can we use the marks on the ruler to measure the length of the pencil?
   Students might comment that the pencil is between 14 and 15 centimetres long.
   Could the little marks (millimetres) between the centimetres help us to be more accurate? What do those ‘in between’ marks mean?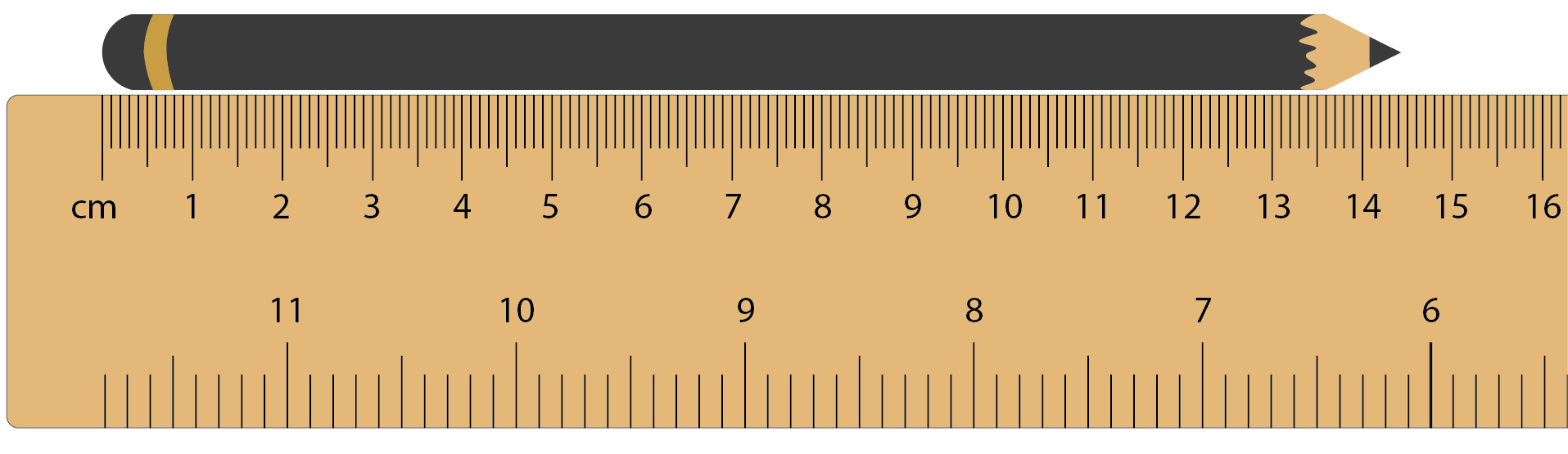
   

2. Some students might know that the smaller marks refer to millimetres. Some rulers have both ‘cm’ and ‘mm’ on the scale. Explain that the prefix "milli-" means one thousandth. Use a 1 metre ruler to demonstrate this.
   How many centimetres are in one metre? Check the end of the ruler to locate 100cm. Each centimetre is one hundredth of a metre. Record this on a class display using words and symbols (e.g. "one hundredth", 1/100).
   How many of these smaller units, millimetres, fit in one centimetre?
   If 100 centimetres make one metre, how many millimetres make one metre? Each millimetre is one thousandth of a metre. Record this on a class display using words, symbols, and equations (e.g. "one thousandth", 1/1000, 10 x 100 = 1000,).
    
3. Create a table of simple conversions of centimetres to millimetres. 
    
4. Use your table to practise converting between measures in mm, cm, and m.
   How many millimetres is the same length as …10 centimetres? …17 centimetres? ...100 centimetres?
   Look for students to use multiplicative knowledge to answer these questions. They might refer back to materials to confirm their thinking, or use a calculator to confirm their answer. 
    
5. Return to the original measurement problem:
   How long is this pencil in millimetres?
   Students might determine the measure by first recognising that 14 cm = 140 mm, before counting on in ones: 141, 142, 143, 144 mm.
   
    
6. Provide other examples of finding lengths in millimetres. In most cases an object does not measure a whole number of centimetres in length. Within this task, consider what groupings will best encourage tuakana-teina and productive learning conversations. It also might be appropriate for some students to work independently, whilst others might benefit from further teacher support.
   For example: Students might measure the lengths of their fingers and answer questions like: How much longer is your longest finger than your smallest finger?

Next steps 

1. Pose problems where the measures are given in both centimetres and millimetres and ask students to choose the appropriate unit to work with. For example: Luke’s pencil is 138mm long and Kayla’s pencil is 9cm long. If the pencils are put end-on-end what is the total length?
    
2. Measure the lengths of objects where the use of metres is required and can be combined with other units for more accuracy. For example, look at the heights of sportspeople. What does 1.83 m mean? How many centimetres is that? If a Silver Fern netballer is 190 cm tall, what is her height in metres?