Chessboard Challenges

In this activity, students are challenged to solve two puzzles involving chessboards. They do not need to know how to play chess to do the problems, but they will need plenty of perseverance! Don’t be put off giving them to your link students; they proved very popular when trialled, and students persisted even when their teachers had given up! If they can’t find the solutions in the time allocated, let them come back to them over several days if necessary.
Puzzle One
Introduce the problem and clarify what it requires by asking:

• How many squares are there on the whole chessboard? (64)
• So how many will be in each piece when you cut it up into four congruent parts? (16)
• Why can’t you just cut it into four 4 x 4 squares? (Because each piece has to have a knight sitting on it.)

Each student will need more than one copy of the copymaster, especially if they are to cut them up. Alternatively they could draw their own 8 x 8 “chessboards” on square grid paper and experiment with these. They should try and use pencil for much of their thinking (rather than scissors): it is much easier to erase a couple of lines
than to make up another grid.

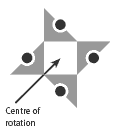
The key to this puzzle is rotational symmetry. A rotation is when an object is turned
about a fixed point, known as the centre (of rotation). A design is said to have
rotational symmetry if, when turned about a point, it fits onto its original position
exactly. For example, this design would fit onto its original position 4 times as it
is rotated through one full turn about the centre. We say therefore that the design
has rotational symmetry of order 4.

If students are unable to get anywhere with the puzzle, try posing a similar but
simpler problem: “Can you cut this shape into 2 congruent pieces so that each piece
has a knight on it?”

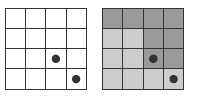
You could also prompt them to think in terms of rotational symmetry by asking them “How could you arrange these 4 congruent pieces (see below) so that they make a complete 4 x 4 square? The first piece has already been put in position.”

Tell your students that the solution to Amy’s grandmother’s puzzle has rotational
symmetry and that the centre of rotation is in the centre of the chessboard.
This information, combined with the partly completed piece shown in the
illustration in the student book, should be enough to set them on the right
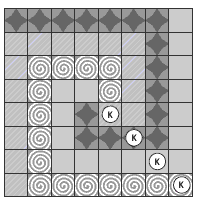
path. If a further clue is needed, show how the board can be divided into four
concentric squares, each with a knight on it, as in the picture at right. This
division suggests (correctly) that the four congruent pieces will each consist
of a quarter of each of the four concentric squares.

Puzzle Two

When students are trying to solve this puzzle, encourage them to use the mathematical words horizontal, vertical, and diagonal. Use them yourself in questions and discussion.
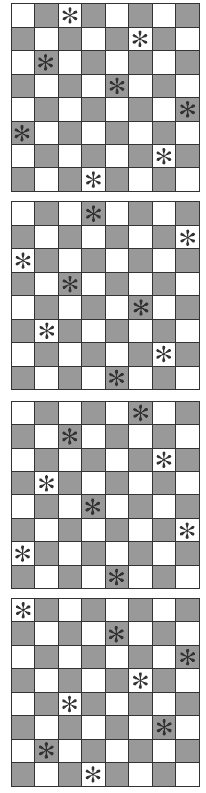
Unlike Puzzle One, which requires an element of inspiration, students can solve  puzzle Two by doggedly moving queens (counters) around until they find a configuration that works. Once the students understand what is required, leave them to try and work it out themselves. If they think they have solved the puzzle, get them to check each diagonal; it is easy to find a “solution” that looks right when it is not. There are 12 distinct solutions to the puzzle (ones that are not just reflections or rotations of another). Once students have found one, encourage them to find another.

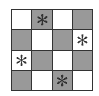
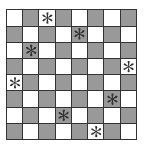
If they are getting nowhere and appear inclined to give up, take them back to a simpler problem: place 4 queens on a 4 x 4 board so that all are safe. The solution is in the diagram on the right.
Talk your students through the simpler problem and then transfer them to the 8 x 8 board. Those who are familiar with chess may realise that if 2 queens are separated by a knight’s L-shaped path (2 steps followed by a 90° turn and 1 more step, or vice versa), each queen is safe from the other.
Of all the 12 solutions to the puzzle, only the one in this diagram shows symmetry. You may like to show it to your students and discuss its special features.

Extension

Sudoku puzzles have certain similarities to the queens puzzle. They use a 9 x 9 grid (not 8 x 8), and the digits 1 to 9 (not queens) have to be placed in every cell in such a way that no digit is repeated in a row or a column. In the case of sudoku, diagonals are irrelevant, but the 9 x 9 grid is subdivided into 3 x 3 subgrids and each digit is allowed to appear only once in each of these small grids. A game board comes with some of the digits already placed. This placement is always symmetrical: rotational and/or reflective. The aim of the game is to complete the board.
Sudoku games don’t require any mathematical knowledge (apart from the ability to recognise the digits 1–9), but playing them helps to develop spatial reasoning, logic, and perseverance. Many teachers have found them an excellent classroom activity. You can find Sudoku puzzles in most daily newspapers or get them from www.nzherald.co.nz/sudoku or paperbacks dedicated to them. They are graded from easy to extremely difficult. This makes them even more ideal for the classroom because different students can work at different levels. But if you plan to introduce them to your students, make sure that you start with the easiest grade. Be warned that these puzzles can be very addictive!

Answers to Activities

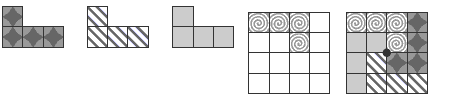
Puzzle One

Puzzle Two
Here are four solutions. There are 12 altogether (not counting rotations and reflections).