These are level 3 measurement and number problems from the Figure It Out series.
A PDF of the student activity is included.
Click on the image to enlarge it. Click again to close. Download PDF (154 KB)
solve problems involving time (Problem 1)
explore fractions of regions (Problem 2)
solve problems using addition and logic strategies (Problem 3)
Problem One
From 12.30 p.m. to 3.30 p.m. is a period of 3 hours. In this time, Stanley’s watch loses 3 minutes. There are eight periods of 3 hours in a 24 hour day, so his watch will lose 8 x 3 = 24 minutes.
As an extension, other time problems could be posed. The difficulty of each problem will depend on the complexity of the rate involved. For example:
“Tania set her watch to the radio time at 12.00 p.m. When she checked later, she noticed that when the announcer said the time was 9.00 p.m., her watch showed 9.06 p.m. How many minutes would her watch gain over a 24 hour period?”
In this problem, the rate of time gain or loss is much more difficult. It can be represented as:
In this case, the watch gains 2/3 of a minute every hour. Students may deduce that in 3 hours, the watch will gain 2 minutes. There are 8 periods of 3 hours in a day, so the total number of minutes gained will be 8 x 2 = 16 minutes.
Problem Two
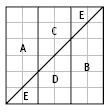
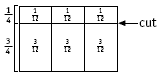
The concept of area is important in this problem. Consider the birthday cake being this size, with the cuts shown and each piece labelled:
Pieces A and B are the largest, with an area of 10 square units. There are 36 square units in total, so these pieces are each larger than a quarter (nine square units). Whà’s cut does not work.
In order to make quarters, Whà must create areas of nine square units, using the area model shown below.
Each piece before Whà’s cut is 12 square units. So three square units must be removed from each piece. This can be done by a horizontal cut as shown. In general, the cut needs to be 1/4 of the way down each third.
Problem Three
For all the stacks to have the same totals, all the numbers must add to a multiple of three: 3 + 4 + 5 + 7 + 10 + 1 + 9 + 6 + 9 = 54.
Dividing 54 by three gives the total needed for each stack: 54 ÷ 3 = 18. The picture shows stack totals of 12, 18, and 24 respectively. To balance these, the
will need to be shifted from the right stack to the left stack.
Problem Four
This type of problem is often referred to as a “Eureka” problem – it requires a flash of insight to solve. You could suggest to students that they “think outside the square”!
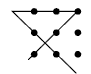
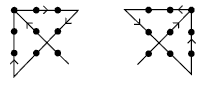
Only four connected lines are allowed and there are nine dots, so each line will need to pass through the maximum number of dots (an average of 2 1/4 dots). If we try to go through the maximum number of dots each time, we might get this:
At this point, the next line can go through only one dot. This will not be sufficient:
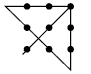
Extending the second line means the This leads to the final solution.
third line goes through two dots.
Answers to Problems
1. 24 minutes
2. a. No. The 2 larger pieces at each end are bigger than the 4 other pieces joined
together.
b.
3. She needs to move the ![]() from the third stack to the first. (Each stack will then
from the third stack to the first. (Each stack will then
total 18.)
4. Two possible solutions