This is a level 5 number activity from the Figure It Out series. It relates to Stage 8 of the Number Framework.
A PDF of the student activity is included.
Click on the image to enlarge it. Click again to close. Download PDF (1001 KB)
multiply decimals
solve problems involving the rate of growth
Number Framework Links
Use this activity to:
• help students consolidate and apply their knowledge of decimal place value (stage 8)
• encourage the transition from advanced multiplicative strategies (stage 7) to advanced proportional strategies (stage 8).
A calculator or spreadsheet program
Activity One
This activity involves exploring and comparing rates of change and requires students to think carefully about how different factors relate to each other.
Begin by revising what happens to the place value of the digits in a whole number or a decimal when it is multiplied or divided by 10, 100, and 1 000. Students need to know that when they multiply a number by 10, the digits move one place to the left in their place value columns and when they divide by 10, the opposite happens. Questions like these can be used to check understanding: 0.15 x 100 = and 10.6 ÷ 1 000 = .
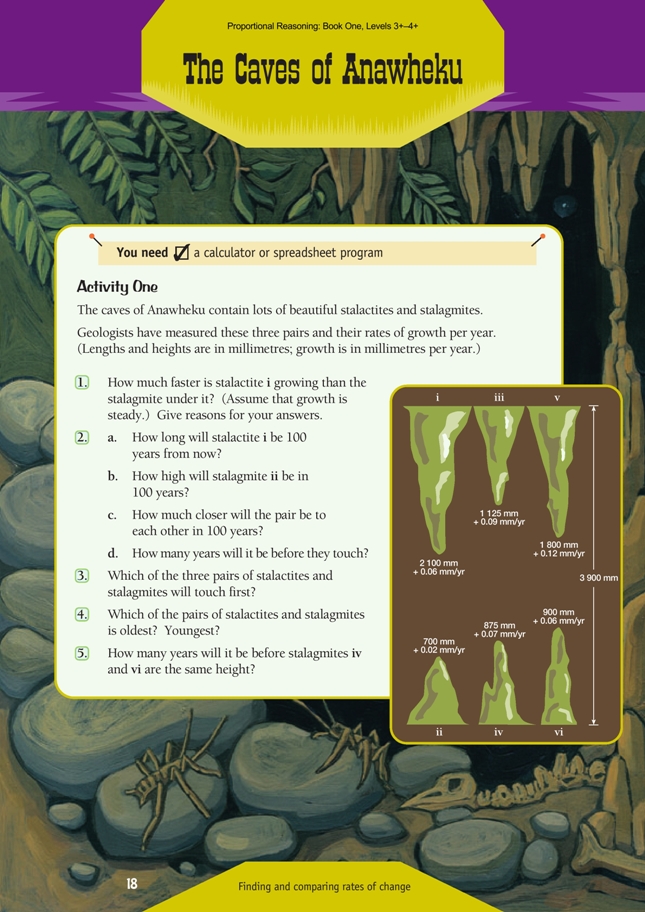
Check that your students can read the diagrams. Questions that you could use to do this include:
• What is the height of the cave?
• How can you work out the size of the gap between a stalactite and its stalagmite?
• How does the diagram tell you the rate of growth of the stalactites and stalagmites?
• Why do the stalactites grow faster than the stalagmites?
In question 1, students need to understand that if stalactite (i) is growing at a rate of +0.06, this means that it is growing by 6/100 of a millimetre each year (mm/yr) and that this is faster than 2/100 of a millimetre per year, which is the growth rate of stalagmite (ii) below it. From there, it is a short move to comparing the rates of growth and answering the question “How much faster …?”
To solve question 2d, students need to see that the stalactite and stalagmite are coming together simultaneously but at different rates, so they are getting closer by 0.06 + 0.02 = 0.08 mm/yr.
If the gap is being reduced by this amount each year, the answer to the question
“How long will it be …?” is answered by dividing the gap of 1 100 mm by 0.08.
You will need to make a judgment call as to whether you want your students to use a calculator to solve the different parts of this activity. Almost all of the calculations involve numbers that are fairly easy to work with, and they are especially suited to part–whole strategies. If you want your students to work without calculators, get them to use the think, pair, and share technique to help them find strategies. You may need to prompt them:
• What do you have to find out to know how long it will take?
• What equation means the same as that?
• If dividing by 0.08 is awkward, what can you do to make it easier?
• Have you got an easy way to divide 1 100 by 8?
One part–whole strategy would go like this: 800 ÷ 8 = 100; 240 ÷ 8 = 30. That leaves 60 ÷ 8 = 7.5. So we have 137.5 lots of 100 yrs, which makes 13 750 yrs.
Before the students start calculating in question 3, get them to use proportional reasoning to predict the answer. They may see that (i) and (ii) are coming together at 0.08 mm/yr while the rate for (iii) and (iv) is 0.16 mm/yr, and for (v) and (vi), 0.18 mm/yr. This last pair is coming together twice as fast as the first pair but the gap is similar; and a little faster than the second pair but the gap is much smaller. Based on this reading, the third pair will join first. Students should then confirm this prediction by calculation and discuss a variety of strategies for doing so.
In question 4, proportional reasoning suggests that the first pair must be the oldest because their total length is greater than that of the other two pairs, but they have been growing at no more than half the rate. To confirm that this is the case, students should simply divide the length of either the stalactite or the stalagmite by its rate of growth. This will give its age in years.
Question 5 should generate some interesting discussions and strategies. Most students will probably start with a trial-and-error method. Show them how to turn this into a trial-and-learn method: under the heading Trial, they could record the statement “(iv) starts at 875 and goes to 882 in 100 yrs, while (vi) goes from 900 to 906.” Under the heading Learn, they could record “over 100 yrs, (iv) gained 1 mm on (vi).” Some will use this reasoning to see the solution immediately, while others will need to do a number of trials.
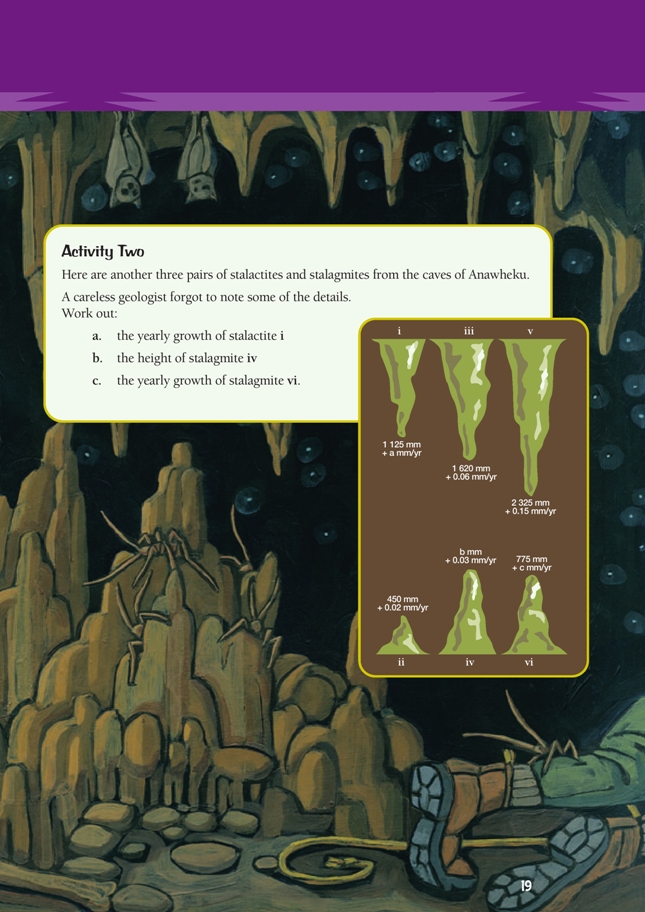
Activity Two
Have the students discuss this question in their problem-solving groups and report back to the class. Direct them to come up with a strategy for solving part a, based on the known facts. The vital connection they need to make is that stalagmite (ii) is the same age as stalactite (i). Once they realise this, they should be able to determine the growth rate of stalactite (i) by dividing its length by its age.
Encourage your students to share their calculation strategies. Assist them with recording by modelling their explanations on a chart or whiteboard.
Answers to Activities
Activity One
1. 3 times. (The stalactite is growing 0.06 mm/yr and the stalagmite 0.02 mm/yr. 0.02 x 3 = 0.06)
2. a. 2 106 mm. (2 100 + [0.06 x 100])
b. 702 mm. (700 + [0.02 x 100])
c. 8 mm. (6 + 2 = 8)
d. 13 750 yrs.
The gap between stalactite (i) and stalagmite (ii) is 1 100 mm (3 900 – [2 100 + 700]). 1 100 ÷ 0.08 = 13 750 yrs.
3. (v) and (vi) will touch first.
The gap between (i) and (ii) is 3 900 – 2 800 = 1 100, and this gap is closing by 0.06 + 0.02 = 0.08 mm/yr. 1 100 ÷ 0.08 = 13 750 yrs.
The gap between (iii) and (iv) is 3 900 – 2 000 = 1 900, and this gap is closing by 0.09 + 0.07 = 0.16 mm/yr. 1 900 ÷ 0.16 = 11 875 yrs.
The gap between (v) and (vi) is 3 900 – 2 700 = 1 200, and this gap is closing by 0.12 + 0.06 = 0.18 mm/yr. 1 200 ÷ 0.18 = 6 670 yrs (rounded to the nearest 10).
4. (i) and (ii) are the oldest pair; (iii) and (iv) are the youngest. (i) and (ii) have been growing for 2 100 ÷ 0.06 = 35 000 yrs. (iii) and (iv) have been growing for 1 125 ÷ 0.09 = 12 500 yrs. (v) and (vi) have been growing for 1 800 ÷ 0.12 = 15 000 yrs.
5. 2 500 yrs. At the moment, the difference is 900 – 875 = 25 mm. Each year, (iv) gains 0.01 mm (0.07 – 0.06 = 0.01) on (vi), so the two should be the same height after 25 ÷ 0.01 = 2 500 yrs.
Activity Two
a. 0.05 mm. (i) and (ii) have been growing for 450 ÷ 0.02 = 22 500 yrs.
1 125 ÷ 22 500 = 0.05 mm.
b. 810 mm. (iii) and (iv) have been growing for 1 620 ÷ 0.06 = 27 000 yrs. 27 000 years of growing at 0.03 mm/yr = 27 000 x 0.03 = 810 mm.
c. 0.05 mm. (v) and (vi) have been growing for 15 500 yrs. 775 ÷ 15 500 = 0.05 mm.