The purpose of this unit is to engage students in applying their knowledge of measurement to solve problems involving food technology.
- Identify, quantify, and represent, using graphs and expressions, the effect of a scale in time contexts.
- Describe, apply, and graph linear relationships to solve problems involving time, temperature, and mass.
- Scale, convert, compare, and apply metric measurements to solve problems involving grams and kilograms.
- Compare and apply time and money measurements to solve relevant problems.
- Apply proportional reasoning to solve problems involving rates.
This unit provides an opportunity for students to apply their skills and understanding of measurement to solve food technology problems involving the interdependence of variables when scaling the components of a recipe.
To ensure maximum engagement and participation in this unit, you should consider your students' prior knowledge in the following areas:
- using scale factors
- calculating percentages of whole numbers
- constructing and analysing data displays
- describing linear relationships
- solving and applying linear equations
- illustrating linear rules on graphs
- scaling, converting, and using metric measurements
- calculating rates.
This cross-curricular, context-based unit has been built within a framework that has been developed, with input from teachers across the curriculum, to deliver the mathematics learning area, whilst encouraging differentiated, student-centred learning.
The learning opportunities in this unit can be further differentiated by providing or removing support to students, and by varying the task requirements. Ways to differentiate include:
- roaming and supporting students in a variety of groupings to ensure they understand the task at hand, the skills needed to succeed, and can apply these skills in a suitable process
- varying the amount of structured scaffolding and guided teaching you provide to students when investigating new tasks
- providing opportunities for students to create their own problems, ideally related to a familiar, relevant context (e.g. catering the food for a class party)
- providing extended opportunities for students to revise and apply learning from throughout the unit
- modelling the application of ideas at every stage of the unit
- strategically organising students into pairs and small groups in order to encourage peer learning, scaffolding, and extension
- allowing the use of calculators to reduce the cognitive load required in each task
- working alongside individual students (or groups of students) who require further support with specific areas of knowledge or activities (e.g. creating a graph, writing a rule).
With student interest engaged, mathematical challenges often seem more approachable than when presented in isolation. Therefore, you might find it appropriate to adapt the food-focused contexts presented in this unit. For example, you might frame each session around food contexts related to an upcoming event (e.g. school camp) or invite students to come up with a shared context (perhaps related to their cultural backgrounds and experiences of preparing and sharing food). You might also change the food products featured in each session to be of increased relevance to your students.
Structure
The first session is an introductory activity that is aimed to spark the imagination of students, to introduce the need for a particular idea or technique in mathematics that would enable them to explore deeper into that context. It is expected that rich discussion may be had around the context and around the nature of the mathematics involved.
Following the introductory session, each subsequent session in the unit is composed of four sections: Introducing Ideas, Building Ideas, Reinforcing Ideas, and Extending Ideas.
Introducing Ideas: It is recommended that you allow approximately 10 minutes for students to work on these problems, either as a whole class, in groups, pairs, or as individuals. Following this, gather the students together to review the problem and to discuss ideas, issues and mathematical techniques that they noticed during the process. It may be helpful to summarise key outcomes of the discussion at this point.
Building Ideas, Reinforcing Ideas, and Extending Ideas: Exploration of these stages can be differentiated on the basis of individual learning needs, as demonstrated in the previous stage of each session. Some students may have managed the focus activity easily and be ready to attempt the reinforcing ideas or even the extending ideas activity straight away. These could be attempted individually or in groups or pairs, depending on students’ readiness for the activity concerned. The students remaining with the teacher could begin to work through the building ideas activity together, peeling off to complete this activity and/or to attempt the reinforcing ideas activity when they feel they have ‘got it’.
It is expected that once all the students have peeled off into independent or group work of the appropriate selection of building, reinforcing and extending activities, the teacher is freed up to check back with the ‘early peelers’ and to circulate as needed.
Importantly, students should have multiple opportunities to, throughout and at the conclusion of each session, compare, check, and discuss their ideas with peers and the teacher, and to reflect upon their ideas and developed understandings. These reflections can be demonstrated using a variety of means (e.g. written, digital note, survey, sticky notes, diagrams, marked work, videoed demonstration) and can be used to inform your planning for subsequent sessions.
The relevance of this learning can also be enhanced with the inclusion of key vocabulary from your students' home languages. For example, te reo Māori kupu such as kauwhata (graph), meneti (minute), ōrau (percent), āwhata (scale), wā (time), putu (degree), taurangi (variable), pānga rārangi (linear relationship), ture (rule, formula), papatipu (mass), karamu (gram), manokaramu (kilogram), and pāpātanga (rate) might be introduced in this unit and then used throughout other mathematical learning.
- Graphing software and/or templates
- Materials to be used to model each problem (optional)
- Calculators (optional)
Introductory Session
This activity is intended to motivate students towards the context and to inform teachers of students' understandings. It utilises mathematical skills and knowledge in the context of food technology.
- Pose the following problem to students.
Baking in bulk or batches?
A café serves cheese scones. A standard mixture takes 15 minutes to prepare, 20 minutes to bake and produces 14 scones. If the mixture is doubled, it needs a further 7 minutes to prepare but takes the same time to bake. The café oven can fit a maximum of 20 scones at a time for even baking.
- What is the percentage time saved by making a double mixture?
- Is it best to bake in bulk or batches (a double mix, or two singles)?
In their reasoning, encourage students to consider the practicalities of the context, food technology, and to include relevant calculations within their reasoning.
- Discuss this activity using the following prompts:
- The best scones are baked immediately after mixing. To produce 28 of the best scones, is it best to bake in bulk or batches?
- The café will be serving the scones throughout the day. Taking this into consideration, is it best to bake in bulk or batches?
- Would the time saved in mixing the ingredients to bake in bulk outweigh the advantages of baking in batches?
Session One
Introducing Ideas
- Pose the following problem to students: The Nouveau-Traditional Café wants to put a twist on ‘golden sausages’, making the dish from one large meat loaf. While a dish made of 6 sausages would only take 25 minutes to bake at 180°C, a single meatloaf made from the same amount of sausage meat takes one hour to cook at the same temperature.
- Explain why the difference in the cooking time.
- Discuss, using the following prompts:
- What physical quantities/variables have been kept the same with the change in the recipe?
- What physical quantities have been adapted in the change from sausages to meatloaf?
- How does the cooking process depend on time? How might this be relevant to the change from sausages to meatloaf?
Building Ideas
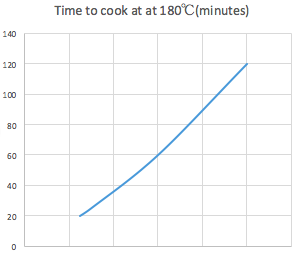
- Explain to students: The cooking time of a meatloaf made in a standard loaf tin depends on the height of the loaf. This has been shown in the graph below. Unfortunately, the scale for the height of the loaf has not been drawn in. A loaf that is 6 cm high takes one hour to cook. A loaf that is 10 cm high takes twice as long to cook as the 6 cm loaf.
- Have students use this information to determine:
- the horizontal scale of the graph
- the cooking time for an 8 cm high loaf.
Reinforcing Ideas
- Explain to students: The cooking time of a sausage, or a meatloaf made from sausage meat, depends on the minimum dimension (length, height or width) of the sausage or loaf.
- Have students do the following:
- graph the cooking time against the minimum dimension of the following sausages/meatloaf
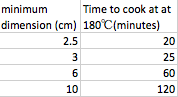
- describe the relationship shown
- consider: what would the cooking time for a meatloaf of width 10 cm, height 6 cm and length 22 cm be?
- consider: what would the cooking time for a meatloaf of width 12 cm, height 8 cm and length 22 cm be?
Extending ideas
- Explain: The cooking time of a sausage, or meatloaf made from sausage meat, depends on the minimum dimension (length, height or width) of the sausage or loaf. A rule that gives a good approximation of the cooking time for a meatloaf in an oven set to 175°C is x2 + x - 13, where x is the length in cm of the minimum dimension of the loaf. With this in mind, have students do the following:
- describe the relationship.
- consider: what would the cooking time for a meatloaf of width 15 cm, height 6 cm and length 25 cm be?
- consider: what would the cooking time for a meatloaf of width 12 cm, height 8 cm and length 25 cm be?
Session Two
- Explain: The chef at the Nouveau-Traditional Café roasts rump beef to a perfect medium-rare based on how big the rump is. The oven is preheated to 135°C and then the roasting is time worked out as 20 minutes and a further 20 minutes for each 500g of beef in the rump.
- What would the roasting instructions for a 1.25 kg rump be?
- Discuss, using the following prompts:
- Would the temperature of the oven be the same or different?
- What is the mass of the rump in grams?
- Should the chef rely purely on this formula?
Building ideas
- Provide time for students to work through the following problems:
- What would the roasting instructions for a 500 g rump be?
- What would the roasting instructions for a 1000 g rump be?
- What would the roasting instructions for a 1500 g rump be?
- Write the rule to give the time to roast a rump, t in minutes, based on the mass, m in g.
- Use your rule to find the roasting time for a 1250 g rump.
Reinforcing Ideas
- Provide time for students to work through the following problems:
- What would the roasting instructions for a 0.5 kg rump be?
- What would the roasting instructions for a 1 kg rump be?
- What would the roasting instructions for a 1.5 kg rump be?
- Write the rule to give the time to roast a rump, t in minutes, based on the mass, m in kg.
- Use your rule to find the roasting time for a 1.75 kg rump.
Extending Ideas
- Provide time for students to work through the following problems:
- Write the rule to give the time to roast a rump, t in minutes, based on the mass, m in g.
- Show this rule on a graph.
- To roast a chicken, the oven is set slightly hotter and the roasting time is given as ten minutes plus a further 20 minutes per 400g. Write the rule to give the time to roast a chicken, t in minutes, based on the mass, m in g.
- Show the chicken roasting rule on the same graph as the rump roast rule.
- Use the graph the two rules to find what mass of meat will have the same roasting time regardless of whether it is rump beef or chicken.
Session Three
Introducing Ideas
- Explain: At the Light-not-Lite café, the mass, in grams, of each of the items on the menu is given. The mini pavlova dessert is popular. The recipe for six mini pavlovas uses 175 g of caster sugar, 3 eggs and 300 g of cream and 50 g of other ingredients. The average mass of an egg is 50 g. What is the total mass of one pavlova in grams?
- Discuss, using the following prompts:
- Will the mass of the ingredients be more, less or the same as the mass of the product? Will this mass be exact or approximate?
- Which ingredient is the least likely to be the same as the mass stated in the recipe?
- Will the mass of one mini pavlova be one sixth of the mass of the full mixture?
Building Ideas
- Provide time for students to work through the following problems:
- A cake served in the Light-not-Lite café has a mass of 1.35 kg. What is the mass of this cake in grams?
- If the cake is sliced into 8 pieces, what is the mass of one slice?
- If the cake is sliced into 12 pieces, what is the mass of one slice?
Reinforcing Ideas
- Provide time for students to work through the following problems:
The recipe for a cake served in the Light-not-Lite café asks for:
- 2 c caster sugar
- 1 ¾ c flour
- ¾ c cocoa
- 2 tsp baking powder
- 2 eggs
- 1 ½ c milk
- ½ c sunflower or soya oil
The Light-not-Lite Café uses the following conversion tables to calculate the mass of the ingredients they use in the kitchen.
| Flour, baking powder, cocoa powder | Caster sugar, oil | Water, milk | |
| Mass (g) of one cup | 130 | 225 | 240 |
| Cup | Tablespoon | Teaspoon |
| 1 | 16 | 48 |
The cake is sliced into 8 pieces for serving in the café. Find the mass, in grams, of one slice of cake.
Extending Ideas
Using the recipe for a cake served in the Light-not-Lite café, and the conversion table given, find the percentage difference in mass of the plain cake compared with the chocolate cake.
Session Four
- Explain to students: At the busy Espresso Express, the average time to prepare coffee has been found as 30 s to prepare a black coffee, 60 s to prepare a coffee with steamed milk and 90 s to prepare a coffee with frothed milk.
- How many steamed milk coffees can be prepared in the same time it takes to make two frothed milk and six black coffee drinks?
- Discuss, using the following prompts:
- Are there any strategies the barista could take to save time?
- Would these have been taken into consideration finding the average time to prepare a particular drink?
Building ideas
- Provide time for students to work through the following problems:
The barista at the Espresso Express is paid at the rate of $24 per hour.
- What is the average labour cost of producing a steamed milk coffee?
- What is the average labour cost of producing a black coffee?
- What is the average labour cost of producing two black coffees?
- What is the average labour cost of producing three black coffees?
- What is the average labour cost of producing a frothed milk?
Reinforcing Ideas
- Provide time for students to work through the following problems:
The barista at the Espresso Express is paid at the rate of $24 per hour.
- What is the average labour cost of producing a frothy milk and a steamed milk coffee?
- How much more is the average labour cost of producing three black coffees than of producing a steamed milk coffee?
- What is the average labour cost of producing two steamed milk coffee and one black coffee drinks?
- The price of a cup of coffee is the sum of the labour costs, the resource costs and the mark up. The café charges $4.50 for a steamed milk coffee. What is the mark up on a steamed milk coffee?
Extending Ideas
The Espresso Express makes coffee continuously during working hours. The average cup of coffee uses $1.50 of resources to produce and then the labour cost the barista of (paid at the rate of $24 per hour) needs to be included. The café charges $4.50 for a steamed milk coffee drink.
- What is the profit on a steamed milk coffee drink?
- If the Espresso Express puts the same mark up on all their drinks, what will the cost of a long black coffee be?
- If the Espresso Express puts the same mark up on all their drinks, what will the cost of a frothy cappuccino coffee be?
Session Five
- Estimating that each person will consume a nibble at a rate of 1 piece every five minutes, how many nibbles do Noble Nibbles need to prepare?
- What factors might affect the rate at which nibbles are consumed?
Building Ideas
Provide time for students to explore the following problems: Noble Nibbles are serving trays of finger food to a function. They have estimated that 90 trays of nibbles are needed.
- How many trays will each of the ten waiting staff take over the course of the function?
- The function lasts for 1 ½ hours. How long is it estimated to take for all the nibbles to be picked off a tray?
Reinforcing Ideas
- Provide time for students to explore the following problems: Noble Nibbles are serving trays of finger food to a function. They have estimated that 3600 individual nibbles are needed.
- Trays of nibbles are laid out in rectangular arrays of 5 x 8 pieces. How many items are there on each full tray?
- How many full trays are needed to provide the 3600 nibbles?
- The waiting staff will take one tray out at a time each, circulating until it is empty, then return to the kitchen for a new tray. If there are ten waiting staff employed for the function, how many trays will each of the waiting staff take over the course of the function?
Extending Ideas
- Provide time for students to explore the following problems: Noble Nibbles need to serve trays of finger food to a function of 200 people. They have allowed for one nibble per person every five minutes, over the 1 ½ hours the function will last. The ten waiting staff leave the kitchen with one full tray each. They will be expected to circulate for ten minutes and then return to the kitchen to replace the empty tray with a new, full one. How many items are on each tray on average?
Dear parents and whānau,
Recently we have been applying our knowledge of measurement to solve problems involving food technology. Ask your child to share their learning with you. Together, you might be able to create a new problem for our class to solve, using a food context that is relevant to your family.