This problem solving activity has a geometry focus.
Ravi enjoyed designing plans for a castle so much that he decided to have another go.
This time, instead of using cubes to make the castle he has used cuboids. (Cuboids are also called rectangular prisms).
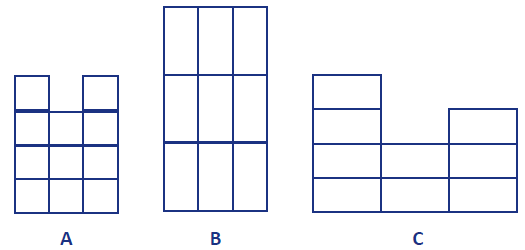
The front view of his new castle is drawing A; the top view is drawing B; and the side view is drawing C.
Build a castle to Ravi’s design using the cuboids.
What is the largest number of cuboids that you can use in the construction of a castle from Ravi’s plans?
What is the smallest number of cuboids that you can use in the construction of a castle from Ravi’s plans?
Can you build a symmetrical castle that is different from any of the ones you have built so far?
How many symmetrical castles can you build to Ravi’s specifications?
Is it possible to design plans for a castle so that it can only be built in one way (uniquely)?
- Construct 3D shapes from 2D drawings.
- Describe the symmetries of 3D shapes.
- Draw 3D shapes on isometric paper.
- Interpret information and results in context; make conjectures in a mathematical context.
- Devise and use problem solving strategies to explore situations mathematically (guess and check, use equipment).
This problem explores the relationship between 2D and 3D shapes and helps students to visualise 3D shapes from 2D representations. It shows that different 3D objects can be represented by the same set of 2D objects. The problem also investigates the symmetry of objects. It extends ideas in the activity The Castle, Geometry, Level 4.
- Copymaster of the problem (Māori)
- Copymaster of the problem (English)
- Small cuboids (any of the Cuisenaire rods from 2-10 can be used for this or longs of the place value blocks)
- Isometric dot paper
The ProblemRavi enjoyed designing plans for a castle The Castle so much that he decided to have another go. This time, instead of using cubes to make the castle he has used cuboids. (Cuboids are also called rectangular prisms). The front view of his new castle is drawing A; the top view is drawing B; and the side view is drawing C. |
- Build a castle to Ravi’s design using the cuboids.
- What is the largest number of cuboids that you can use in the construction of a castle from Ravi’s plans?
- What is the smallest number of cuboids that you can use in the construction of a castle from Ravi’s plans?
- Can you build a symmetrical castle that is different from any of the ones you have built so far? How many symmetrical castles can you build to Ravi’s specifications?
- Is it possible to design plans for a castle so that it can only be built in one way (uniquely)?
Teaching Sequence
- Introduce the problem – create a scenario that the students are builders who have been given the task of constructing a castle from a set of plans. Make sure that the students understand how to use the 2D views and the isometric paper.
- Ask the students to think about what it might look like before giving them the cuboids to work with. Discuss these ideas.
- Give cuboid blocks to pairs of students.
- As the students work ask questions that focus on their construction of 3D shapes from 2D views:
Which face have you started with? Why?
How do you keep track of the faces that you are building?
Does the castle look like you thought it would? (How is it different?)
Do you find isometric paper helpful for drawing the model?
How would show someone how to use isometric paper for the first time? - Share designs
Extension
On a base of three cuboids by three cuboids, design your own construction using top, side and front views only. Ask the questions above about your design.
Now try a four by four base. What design will give you the biggest difference between the largest number of cuboids you can use and the smallest number?
Solution
The castle with the most cuboids has 26 cuboids. The reason that we have to have 26 cuboids is as follows. First, we are trying to put in as many cuboids as possible. Second, from C we see that we should put two layers on the bottom each with 9 cuboids. Third, also from C there has to be a tower 4 cuboids high but from A we see that there are two such towers with a lower level between them – this gives 2 more on each side and 1 in the middle. Fourth, from C we see that we need another cuboid on the left hand side – this adds another 3 cuboids across the castle from us. No more cuboids are forced. Altogether then we get 26 cuboids.
The castle with the least number of cuboids has only 18 cuboids. To see that we need at least 18 first look at A. This shows 11 cuboids that have to placed somewhere in the castle. Second, look at B. At most three of these cuboids could be seen in A so we need to add a further 6. Third, look at C. There is one more cuboid here (on top of the middle column), that hasn’t so far been taken care of. This gives a total of 18.
Adding two cuboids on to the row with a ‘bump’ nearest to you can produce a symmetrical castle. It is only possible to have one axis of symmetry here.