This problem solving activity has an algebra focus.
There is a pyramid of cannon balls on a pirate ship. The first layer looks like this when you look down on it from above.
How many cannon balls are there in the bottom layer?
How many cannon balls will there be in the second layer?
How many cannon balls will there be in the third layer?
How many cannon balls in the top layer?
How many cannon balls do you need to complete the pyramid?
- Identify a pattern and describe this using their own words.
- Use equipment appropriately when exploring mathematical ideas.
- Devise and use problem solving strategies to explore situations mathematically (guess and check, make a list).
In this problem, students further develop 'a feel for' 2- and 3-dimensional objects. The problem introduces and explores triangular numbers, as the cannon balls in each layer of the pyramid form an equilateral triangle.
In order for the cannon balls to sit on top of each other, the students need to see that one ball will comfortably fit on top of three others. This is best modelled this using tennis balls or oranges.
Triangular numbers become of more interest in higher levels when students explore square numbers, pentagonal numbers and so on. The pictures below show why these numbers are named after geometric objects.
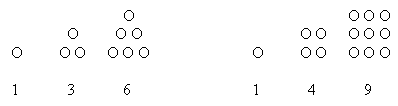
The first three triangular numbers The first three square numbers
In the secondary school, triangular numbers are part of the family of Binomial Coefficients. These numbers have a major part to play in counting, and are vital to probability and statistics generally.
- Copymaster of the problem (Māori)
- Copymaster of the problem (English)
- Poem, story, song, or video about pirates (to engage students in the context)
- Tennis balls or other suitable round objects (e.g. play dough, oranges) to build the pyramid
The Problem
There is a pyramid of cannon balls on a pirate ship. The first layer looks like this when you look down on it from above.
How many cannon balls are there in this layer (the first layer)?
How many cannon balls will there be in the second layer?
How many cannon balls will there be in the third layer?
How many cannon balls in the top layer?
How many cannon balls do you need to complete the pyramid?
Teaching Sequence
- Introduce the problem with your chosen song, video, poem, or story.
- Show students the "cannon balls" (tennis balls or similar). Ask the students to think of ways that they could stack the balls.
- Read problem. Check that the students understand the meaning of the word 'layers' and also know how the pirates piled up their cannon balls.
- Ask the students to guess how many cannon balls they will need. Record the estimates to check against later.
- Brainstorm ways to solve the problem. Link the suggested methods to problems students have solved before.
What strategies could you use?
What equipment will you need?
How will you record your information?
What do you have to find out? - As the students work, ask questions that focus on the patterns they are using to solve the problem.
What can you tell me about the cannon balls?
How are you keeping track of the number of cannon balls? - Share solutions
Extension
If the pirates wanted to put another layer of cannon balls on their pile, they would need to lift up the pyramid and put another layer on the bottom. How many cannon balls would there be in this layer?
Solution
In the first layer there are 1 (across the top) + 2 and 3 (across the middle two rows) + 4 (four at the bottom) = 10 cannon balls.
In the second layer there are 1 + 2 + 3 = 6 cannon balls.
In the third layer there are 1 + 2 = 3 cannon balls.
There is only one cannon ball in the top layer.
All together there are 10 + 6 + 3 + 1 = 20 cannon balls.
Solution to the extension
There would need to be 5 cannon balls in the new layer, if the layer was placed underneath the present bottom layer. The cannonball pyramid would then have 1 + 2 + 3 + 4 + 5 = 15 cannon balls.
