This is a level 4 measurement activity from the Figure it Out series.
A PDF of the student activity is included.
Click on the image to enlarge it. Click again to close. Download PDF (427 KB)
sovle problems involving measurement units
aluminium cans
scales
FIO, Level 3-4, Measurement, Can You? page 5
calculator and ruler
In these activities, students work with the length, mass, and volume of a single object to find the length, mass, and volume of a large number of these objects.
Activity One
For questions 1, 2b, and 2c, encourage the students to express the answer in a variety of units so that they can see the relationship between centimetres and metres, grams and kilograms, and millilitres and litres. You could challenge some students to express the lengths in kilometres (0.09375 kilometres) or the volume in kilolitres (0.26625 kilolitres).
For question 2a, the students may find it difficult to get an accurate reading on the scale if they only weigh one can at a time. Encourage them to try a variety of techniques to find a more accurate measure.
Discuss the methods that the class come up with. For example, they could weigh 10 cans and divide by 10 to find the average mass. This should reduce the errors made by weighing one can at a time.
Activity Two
In this activity, students estimate rather than calculating more exactly as they did in Activity One. For example, in question 1, they can explore different strategies for estimation. Some may round up the 3 500 000 people to 4 000 000 and find 1/4 of this, which is 1 000 000. If they do this, ask them if they can think of a more accurate method, such as rounding 3 500 000 to 3 600 000, which is easily divided by 4. This answer would be 900 000. Others may reduce 3 500 000 to 3 200 000. Their estimate would then be 800 000.
Discuss which strategy gives the closest estimate. Explore the idea of finding the average of the estimates for a more accurate answer. For example:
900 000 + 800 000 = 1 700 000
1 700 000 ÷ 2 = 850 000
In question 2a, the students predict the product of 750 (the number of cans used by each household) times their answer to question 1. Some may realise that 750 is 3/4 of 1 000 and so work out 3/4 of, say, 800 000, which is 600 000, and then multiply this by 1 000 to make 600 000 000. Others may round 750 to 800 and then multiply 800 000 or 900 000 by 800 and get 640 000 000 or 720 000 000 as an answer.
A good technique would be to round up 750 to 800 and then use the lowest estimate of question 1 (800 000): 800 x 800 000 = 640 000 000. This technique of using one high estimate and one low estimate reduces the error caused by rounding and gives a very accurate estimate.
Once again, the calculation in question 2b will depend on earlier estimates and the students’ answers to questions 2a and 2b in Activity One. Have the students explain their thinking and calculation. Make sure that they use the correct unit in the answer.
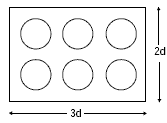
For question 3, the students can either measure a real six-pack or work out the diameter of a can and calculate the volume. The calculation would be (3 x the diameter) x (2 x the diameter) x 125 (the height) plus a little for spacing for the six-pack.
Answers to Activity
Activity One
1. If the length of all the cans is 12.5 cm (standard can size), 750 cans would measure 93.75 m (9 375 cm).
2. a. Answers will vary. You could weigh a number of empty cans to get a mass you
can actually measure on the scales (a can weighs approximately 18 g), or you could
weigh a full can and subtract the mass of the liquid.
b. Approximately 13.5 kg (13 500 g)
c. 266.25 L (266 250 mL).
Activity Two
1. Between 800 000 and 900 000. (A more precise answer is 875 000.)
2. a. Answers will depend on those given for question 1. (Based on the more precise
answer for question 1, an exact answer is 656 250 000.)
b. Answers will depend on those given for question 1. (The exact answer in kg is
11 812 500 kg.)
c. Answers will vary, again depending on earlier estimates and whether you allow
for the cardboard (many cans in six-packs are joined by plastic). Using the
measurements given at the start of the activity (and not allowing for the
cardboard), the volume of one six-pack would be 2 700 cm3 (18 cm x 12 cm x
12.5 cm). So for 109 375 000 six-packs (656 250 000 cans), the volume would be
295 312.5 m3 (295 312 500 000 cm3).