This is a level 4 number activity from the Figure It Out series. It relates to Stage 7 of the Number Framework.
A PDF of the student activity is included.
Click on the image to enlarge it. Click again to close. Download PDF (231 KB)
use place value knowledge to check calculations
Number Framework Links
Use this activity to:
• help students apply advanced additive part–whole strategies (stage 6) in addition and subtraction of large numbers
• help students apply advanced multiplicative part–whole strategies (stage 7) in multiplication and division.
A calculator
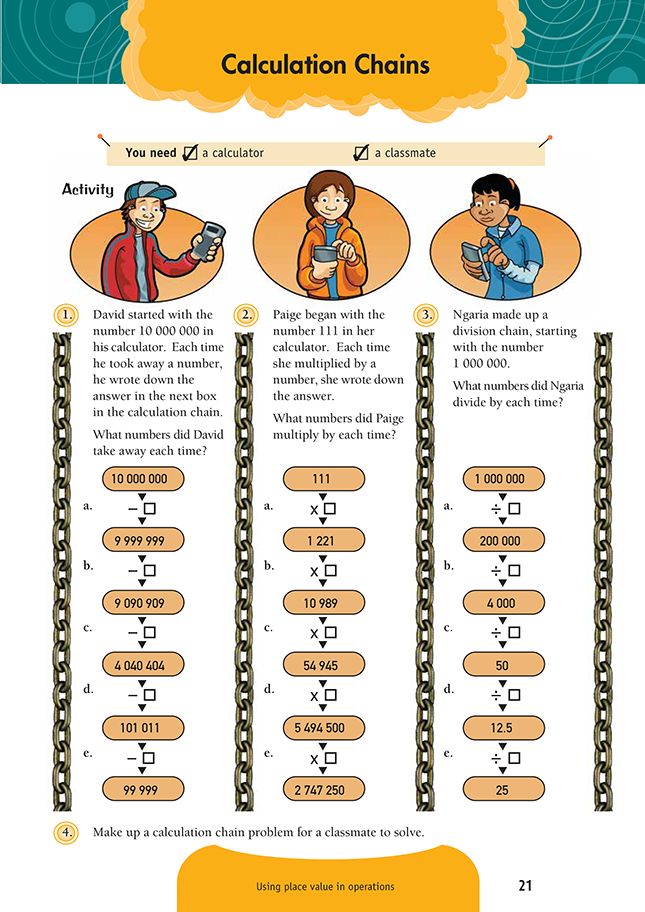
FIO, Level 3, Number Sense and Algebraic Thinking, Book One, Calculation Chains, page 21
A classmate
In this activity, students apply number sense and their knowledge of place value to work out how a number has been transformed on a calculator. Number sense principles that may be explored through this activity include whether a number gets bigger or smaller when it’s multiplied or divided by a whole number or by a decimal number.
Question 1 is useful for students who are working at stage 6. To be able to apply appropriate number sense to questions 2 and 3, students should be making the transition to stage 7 or be already working at this level, although it is possible to benefit from the activity through trial and improvement with a calculator.
Some students may need encouragement to try a strategy beyond guessing and checking on the calculator. Possible strategies to solve 111 x = 1 221 include:
• Estimation: “I know 111 x 10 is 1 110, so it has to be a little more than that.”
• Opposite operation or working backwards: “I’m going to use the opposite operation and work out 1 221 ÷ 111.”
• Looking at the ones place: “The product in 111 x = 1221 suggests only a 1 is possible in the ones place of the box number.”
Encourage the use of these strategies by asking questions such as:
Try estimating what would go in the box before you try it on the calculator. Do you think the answer you get on your calculator is going to be more or less than your estimate? Why?
What happens to a number when you multiply it by 10? 100? 1 000?
What happens to that number when it is divided by 10? 100? 1 000?
What facts do you already know that might help you estimate the answer?
Could you use a tidy number strategy to help you estimate the answer?
What’s the opposite of adding, multiplying, or dividing? How might using the opposite operation help?
Could you use the answer and work backwards?
Extension
In question 3e, some students will be surprised that you can divide 12.5 by something and get a bigger number (25). This could start an interesting investigation:
When you multiply a number by another number, does the first number always get bigger?
When you divide a number by another number, does the first number always get smaller?
Note that Branching Out (pages 10–11 of the student book) raises the same issues.
Answers to Activity
1. a. 1
b. 909 090
c. 5 050 505
d. 3 939 393
e. 1 012
2. a. 11
b. 9
c. 5
d. 100
e. 0.5
3. a. 5
b. 50
c. 80
d. 4
e. 0.5
4. Problems will vary.