Building with triangles
In this unit, students will construct three-dimensional objects with triangles with emphasis on
- identifying properties of triangles
- constructing triangles (both equilateral and irregular), using either ruler and protractor or ruler and compass
- identifying three-dimensional objects which can be constructed using triangles
- designing the net and making three-dimensional objects
- naming three-dimensional objects
construct triangles with specified dimensions using two different techniques
design and construct nets for three-dimensional objects
name basic three-dimensional objects, especially those made with equilateral triangles
This unit explores some aspects of three-dimensional geometry as well as techniques for the construction of triangles.
Getting Started
- Brainstorm with the class ”The properties of triangles”.
Facts you should get include;
Three sides
Three angles/corners
Angles add to 180o
Different types (scalene/isosceles/equilateral/right-angled) - Beware of students saying that triangles have all sides the same length or all angles the same. This is not a property of triangles, but a property of regular polygons (including equilateral triangles). Ensure that this is emphasized.
- Ask students how they could construct an equilateral triangle. Discuss their ideas – their advantages and disadvantages. There are three relatively easy methods, give students the opportunity to try each (or demonstrate each to the class on the board).
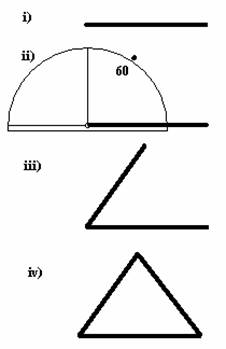
- Using ruler and protractor
- Draw one side to the required length, using a ruler.
- Measure an angle of 60 degrees from one end of the first side.
Draw a second side to the same length as the first, again using a ruler. - Connect the ends, measuring to ensure the third side is the same length as the first two.
-
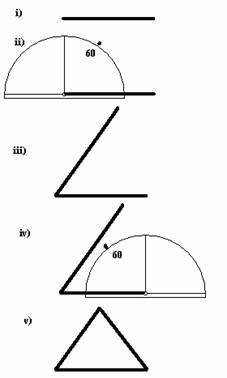
Using ruler and protractor
-
Draw one side to the required length, using a ruler.
-
Measure an angle of 60 degrees.
-
Draw a second side through your mark at 60 degrees.
-
Measure another angle of 60 degrees from the other end of your first side.
-
Draw the third side and rub out any extra lines.
-
Using ruler and compass
-
Draw one side to the required length, using a ruler.
-
Set your compass to a radius equal to the length of the side. Put the point of your compass on one end of the side you have drawn and lightly draw a small arc about where you think the third corner should be.
-
'Move the point of your compass to the other end of your first side and draw another arc, which should cross the first.
-
The point where the arcs cross is the third corner – draw in the remaining two sides, checking they are the correct length as you do so.
.jpg)
- Discuss whether you could use each method to construct triangles if the sides are not all the same. Get students to list advantages and disadvantages of each method, and decide which method is the best.
Method a) can be used to construct triangles as long as you know two side lengths and one angle.
Method b) can be used to construct triangles as long as you know two angles and one side length.
Method c) can be used to construct triangles as long as you know the lengths of all the sides.
Method c) is probably the easiest and most accurate, since measuring with a protractor is likely to produce errors. - Give students the opportunity to practice constructing a variety of triangles using all three methods.
- Show students a model of a tetrahedron.
- Ask them to identify what kind of shape and how many it is made up of (4 equilateral triangles).
- Challenge them to construct the net for a tetrahedron (on paper first to avoid wasting card).
- Check the nets that are drawn. There are two layouts of four equilateral triangles that will fold to make a tetrahedron and one that will not. Get students to identify why (two of the triangles fold to be on top of each other, so there is an open side).
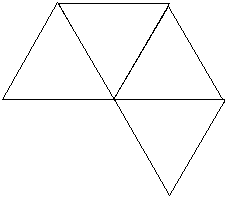
- Allow students to make a model of a tetrahedron from card. Students should either join edges with selotape, or if they wish could include flaps on their net and glue the edges.
- Challenge students to make a different three-dimensional object from only equilateral triangles.
|
4 sides: tetrahedron
6 sides: triangular dipyramid (glue two tetrahedra together)
8 sides: octahedron
10 sides: pentagonal dipyramid (glue two pentagonal pyramids together)
12 sides: snub disphenoid (split a tetrahedron into two wedges and join them with a band of eight triangles)
14 sides: triaugmented triangular prism (attach three square pyramids to a triangular prism)
16 sides: gyroelongated square dipyramid (attach two square pyramids to a square antiprism)
20 sides: icosahedron
24 sides: stellated octahedron (attach a tetrahedron to each face of an octahedron)
|
- Discuss the three platonic solids that can be made from equilateral triangles. How many of these has your class made?
| A platonic solid is a polyhedron all of whose faces are congruent regular polygons, and where the same number of faces meet at every vertex.
In other words, a platonic solid is a three dimensional shape where each face is an identical flat shape with all sides and angles the same, and the same number of these faces meet at each corner.
There are 5 platonic solids, the cube (6 squares, 3 meeting at each vertex), the tetrahedron (4 triangles, 3 meeting at each vertex), the octahedron (8 triangles, 4 meeting at each vertex), the dodecahedron (12 pentagons, 3 meeting at each vertex), and the icosahedron (20 triangles, 5 meeting at each vertex).
|
- Look at some of the other objects students have made. Try to name them.
- Challenge students to make an object that uses equilateral triangles in combination with a different shape. Point out that all the side lengths will need to be the same, even if the shapes are different.
More able students could again be challenged to see how many different objects they can make. Can they name them?
|
pyramid (4 triangles and 1 square)
pentagonal pyramid (5 triangles and 1 pentagon)
triangular prism (2 triangles and 3 squares (or rectangles))
cuboctahedron (8 triangles and 6 squares)
icosidodecahedron (12 pentagons and 20 triangles)
truncated tetrahedron (4 hexagons and 4 triangles)
truncated cube (6 octagons and 8 triangles)
square antiprism (2 squares and 8 triangles)
|
Less able students could be supported either by help in designing the net to make a triangular prism (2 equilateral triangles joined by three squares), or they could be provided with the net to cut out, fold and stick together.Some nets you can print from the attached files and use are: triangular prism, pyramid, pentagonal pyramid, cuboctahedron, truncated tetrahedron, truncated cube, icosidodecahedron.
- Talk about the three types of pyramid (bases: triangle, square, pentagon). Has your class made all three? What do you call a pyramid with a triangle base? (tetrahedron) Could you make a hexagonal pyramid? (No) Why not? (the six equilateral triangles would lie flat on the hexagon and the object would be flat. Note: You can make a hexagonal pyramid, but not with equilateral triangles, you need to use isosceles triangles.
- Look at some of the other objects students have made. Try to name them.
- Ask students to name as many three-dimensional objects as they can which can be made using equilateral triangles.
- Can anyone think of ways we could group these objects? (Number of sides, other shapes used, symmetry)
The most obvious way is to group the objects into those that use exclusively triangles and those which include other shapes in combination with equilateral triangles. - Try grouping the models the class has made using some of these criteria.
There is an abundance of information on polyhedra on the internet. If you require more background or extension material, try these sites:
This week in class we have been investigating making shapes with triangles. Try asking your child how to draw a triangle. See how many different ways they can explain to you. Ask them the names of some three dimensional objects that can be made using triangles. Maybe you could make some at home.
| Attachment | Size |
|---|---|
| truncated_tetrahedron.pdf | 4.95 KB |
| octahedron.pdf | 3.43 KB |
| icosahedron.pdf | 5.5 KB |
| pentagonal_pyramid.pdf | 2.74 KB |
| pyramid.pdf | 5.39 KB |
| triangular_prisms.pdf | 4.9 KB |
| truncated_cube.pdf | 10.59 KB |
| icosidodecahedron.pdf | 12.31 KB |
| cuboctahedron.pdf | 6.49 KB |
Similar Resources
Ruler and Compass Constructions
In this unit we discover how to use rulers and compasses to construct perpendicular lines and to bisect angles. These constructions are used to make a variety of polygons.
I'm So Sorry I Ate Chocolate
This unit explores the magnitudes of sides and angles of a triangle and leads to the discovery and proof of the Sine Rule. This Rule is then used to solve triangles, some of which arise in practical situations. Finally we compare the use of the Sine Rule and the Cosine Rule.
Note that this unit may contain more material than you need for some classes. You may want to choose only some of the sessions if you have not planned to allot five sessions on the Sine Rule and its relation to the Cosine Rule.
Using Trigonometry
In this unit, students will explore the use of trigonometry to find unknown sides and angles in right-angled triangles, taking the concepts that were developed in the previous unit Introducing Trig and looking at different ways of practising the new skills. Students will then develop and reinforce skills to solve practical problems in trigonometry using the problem solving model
reality 
model 
solution 
check
It is important that good algebraic skills are used in setting out their work, and students can be encouraged to practice these individually and using cooperative logic problems in a group situation.
Quadrilaterals
In this unit we conduct a couple of investigations looking at the relationship between the angle between two diagonals of a quadrilateral, the sides of the quadrilateral, and the type of quadrilateral. The main emphasis is on rectangles.
Trigonometric Applications Outside the Classroom
This unit follows on from others that introduce students to sine, cosine and tangent. In this unit students will gain practical experience in using trigonometry in practical situations; mainly outside the classroom.
