This problem solving activity has a logic and reasoning focus.
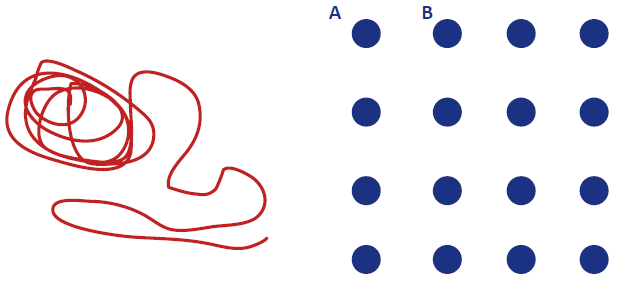
Brian has a pegboard with 16 pegs in a 4 by 4 square array (see the diagram).
He also has a piece of string that he wants to put from the top left hand peg A, to the neighbouring peg B, so that it touches all of the other pegs on the way.
If the string is never put diagonally between the pegs, how many different ways can Brian string up his pegboard?
- Use a systematic approach to count a set of possible outcomes.
This problem challenges students in two ways. Firstly, they are challenged to be systematic and careful in their approach to, and recording of work, in a novel situation. This is an important aspect that is fundamental to all mathematics. Many students record their working in a haphazard way as they go along. This may lead to errors when students lose track of where they are and what they have done.
Secondly, this problem highlights the need to count in a situation that is new to them. Counting is a fundamental part of probability. To determine theoretical probabilities accurately, a knowledge of counting techniques is extremely important. Counting is found in an area of mathematics called combinatorics.
In this problem a guess and check strategy can be used. However, such an approach cannot guarantee that all outcomes have been obtained. Guess and check is nonetheless a good first strategy that will give the students an idea of the problem, along with some possible properties of the problem that they can use in a more systematic approach. However, students should be supported and encouraged to see that there is a better way to try to solve the problem. One way to do this is to help them to see where there are choices, and then to see what implications these choices have. (See the solution.)
- Copymaster of the problem (English)
- Copymaster of the problem (Māori)
- Pegboards and string (or a digital tool - search for interactive pegboard)
The Problem
Brian has a pegboard with 16 pegs in a 4 by 4 square array (see the diagram).
He also has a piece of string that he wants to put from the top left hand peg A, to the neighbouring peg B, so that it touches all of the other pegs on the way. If the string is never put diagonally between the pegs, how many different ways can Brian string up his pegboard?
Teaching Sequence
- Provide students with pegboards to explore.
- Introduce the problem. The problem Pegboard I, Level 3 could be used as an introduction.
- Ask students to suggest a systematic approach to finding a solution.
- As the students work in their groups to solve the problem, continue to encourage them to be systematic.
- Check the progress of each group. Give assistance where needed.
- Pause as solutions emerge and share some of these.
- Pose the extension problem as and when appropriate.
- Share and discuss solutions, recording methods and explanations.
Extension
Suppose that P is the bottom right hand peg. How many ways can Brian join the string from peg A to peg P so that each peg is used and so that the string is always vertical or horizontal between neighbouring pegs?
Further investigations could name any pair of pegs and see if they can be joined by string in a way prescribed, or try pegboards with more pegs.
Solution
Exploring Brian’s Pegboard I (see Logic and Reasoning, Level 3) first may be helpful.
A systematic approach could be:
Starting from A go to E. (B is the final destination once the rest of the board has been navigated.)
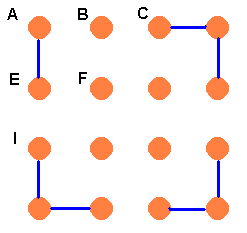
Now there are two ways that Brian might move away from E. He could either go to F or to I. Let’s treat each of these separately. These can be thought of as two branches of a tree diagram.
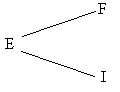
Case 1, E to F: From the diagram we see that EF forces BC. After all we can’t go in to B from F because we haven’t joined all of the pegs up at this stage. We are also forced to join I to J.
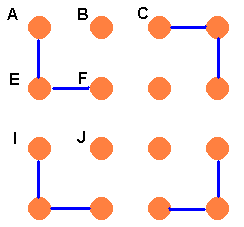
At this point Brian has the following position:
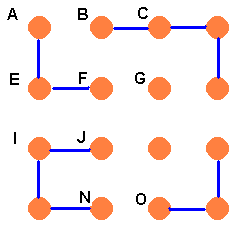
Now notice that J can’t be joined to N. This forces NO to be joined.
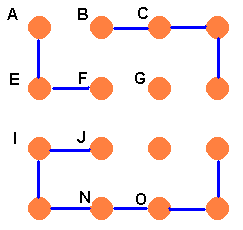
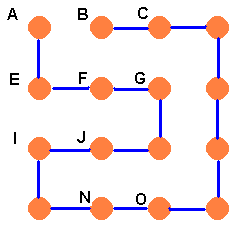
At this point there are two possibilities for F. It can join G or J. In each case there is only one stringing that Brian can make. So Case 1 gives us the two possibilities below.
Case 2, E to I:
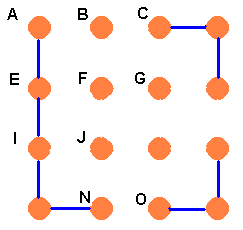
At this point we can either get into B via C or F. So this gives us two subcases.
Again we can think of this as being two more branches of the earlier tree diagram
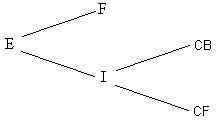
Case 2.1, CB:
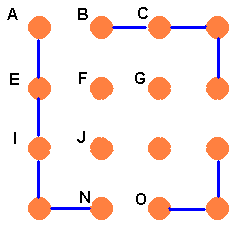
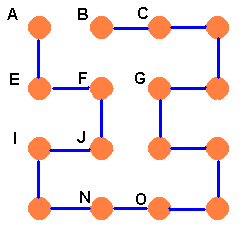
Now F cannot join B so F has to join both G and J. But there are still two choices for G. It can either go to H or to K. Brian would then get the two situations shown below.
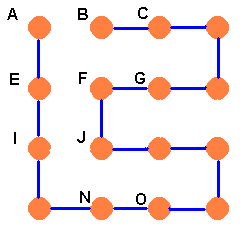
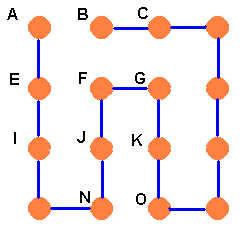
Case 2.2, FC: Using all the old types of argument, this gives the two further stringings below.
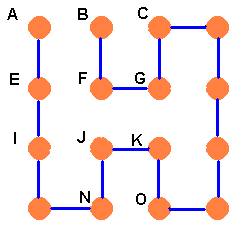
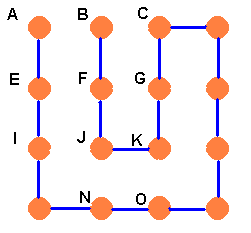
Brian can string his pegboard up in six ways.
Solution to the Extension
There is no way that Brian can join A to p going through all of the other pegs and keeping the string horizontal or vertical between pegs. There are many ways to show this but the quickest is probably to colour the pegs as if they were squares on a chessboard. We show this in the diagram by using x and o. Now, when we join two pegs with string, we are always joining an x to a o. To get from A to P we have to start and end with an x and we have to pass through 16 pegs altogether. You can’t have an alternating sequence of eight xs and eight os that ends in an x!
| A | x | o | x | o | |
| o | x | o | x | ||
| x | o | x | o | ||
| o | x | o | x | P |
This raises the question as to which pegs you can string to A and in how many ways you can do it.