This unit explores the relationships between fractions and decimals. A decimat model is used to explore how fractions arise from equal sharing and how the decimal place value system is a restricted form of equal sharing. The main objective is to link students’ knowledge of fractions with the decimal system.
- Represent common fractions as decimals and vice versa.
- Relate decimals to decimat models that represent their size and composition.
- Combine and partition decimal place values to flexibly add and subtract decimals.
This unit builds on the idea that the need for fractions and decimals arises from division situations, in which ones (wholes), do not give an adequate degree of precision. Lack of closure of a whole number under the operation of division creates the need for rational numbers. The division situations can be either partitive (sharing) or quotative (measuring). In this unit sharing of a decimat model is used to connect fractions and decimals.
Specific Teaching Points
Decimals are a restricted form of equivalent fractions. For example, three quarters is represented in decimals as 0.75 because 3/4 = 75/100. As with whole numbers the place values in decimals are connected although separate columns are used to write numbers. For example, 0.75 has can be expressed in different decimal forms, such as 7 tenths and 5 hundredths, 75 hundredths, 750 thousandths, 7.5 tenths, etc. Flexibility in the way students think about decimal place value supports their fluency with calculation. Central to fluency is students’ understanding of how decimal place value units can be partitioned and combined. For example, 2.3 – 0.7 requires a one in 2.3 to be partitioned into 10 tenths if subtraction is used, or 10 tenths to be combined to form a one if adding on from the 0.7 is used.
The learning opportunities in this unit can be differentiated by providing or removing support to students and by varying the task requirements. Ways to support students include:
- providing physical materials (e.g. decimats), so that students can anticipate actions, model their thinking, and justify their solutions
- connecting decimat models with symbols,
- using calculators to confirm answers, and to look for counting patterns, e.g. 0.5, 1, 1.5, 2, …
- using important mathematical vocabulary to discuss concepts, in particular words for fractions (numerator, denominator) and decimals (tenths, hundredths, thousandths, etc.), and equality/equivalence
- encouraging students to collaborate in small groups and to share and justify their ideas
- altering the complexity of the fractions and decimals that are used. Fractions that can be expressed as tenths and hundredths are easier than those requiring thousandths or further decimal places. Recurring decimals like 0.333... may provide a significant challenge for more knowledgeable students.
The context for this unit is chocolate bars. Students usually find the context engaging. Sharing food is a common practice across cultures worldwide. Investigating the origins of chocolate will lead to finding out about Aztec culture from Central America. However, using foods as a context is sometimes not appropriate for students. In that case, use a context that is relevant and appropriate to your students. For example, the story could be changed to reflect different situations about area (e.g., land, kumara patches), precious sheets of gold or tablets of clay (as in an Indiana Jones film), or space available on school fair tables. Vary the context while retaining the important decimat model.
Te reo Māori vocabulary terms such as taurea (multiply), whakawehe (divide), hautau waetahi (unit fraction), hautanga ā-ira (decimal fraction), and hautanga ā-ira (equivalent fraction) could be introduced in this unit and used throughout other mathematical learning.
Prior Experience
Students would benefit from previous experience with fractions. In particular, they would benefit from experiences of partitioning of areas to form equal parts and the naming of collections of those equal parts as non-unit fractions. This unit uses an area model, the decimat, that is based on tens frames used for whole number place value. It is expected that students will understand whole number place value in a flexible way. They are expected to see place value as a nested system. Within this, they should understand that place value units are nested in others. For example, 23 tens are nested within 230. Therefore, 230 can be renamed as 23 tens. It is also expected that students will have a range of strategies for solving addition and subtraction problems with whole numbers, that include using standard place value (hundreds, tens and ones, etc.) and tidy and/or compatible numbers (rounding and compensating).
Session One
- Show the students a copy of the Breakaway Chocolate bar (Copymaster 1). You may like to house paper copies in the coloured sleeve provided so the chocolate bar looks more authentic. Ask the students why the bar might be suitable to share between two or ten people as is claimed on the wrapper. Students might say that the bar is about the right size or it divides easily into two or ten equal pieces. Slide out the paper ‘bar’ and ask the students what they notice about the snap lines. Discuss how the lines might be used to share a bar into either halves or tenths.
So imagine we share the bar equally among ten people, how much bar does each person get? How could we record this mathematically? - Students may need to connect to story shells such as “Bindi's family collects 24 kūtai (green-lipped mussels) from the beach. The mussels need to be shared equally amongst the 6 family members. How many mussels should each person get?” Similar problems may support students' understandings of the chocolate sharing being expressed as division.
Ways to express the division answer quotient are: 1÷10 = 1/10 or 1÷10 = 0.1
(A scientific calculator provides both decimal and fraction answers) - Ask the students to express the sharing between two people as division: 1÷2 = 1/2. “What is the decimal for one half?” Most students know that 0.5 is the decimal for one half though many are unaware of why that is true. “If two people share the bar, how many tenths do they get each?” (five tenths - half of the bar). So the five in 0.5 means, 5 tenths. So, 1÷2 = 5/10 = 0.5 . You may need to use the pattern of dividing by ten to extend the decimal places to the right beyond what your students are used to.
- Extend the problem by asking, “What would happen if ten people shared three of these bars equally?” You may need to act out the fact that each person could get one tenth from each bar. So the sharing could be recorded as 3÷10 = 3/10 or 3÷10 = 0.3. Consider whether the students can generalise that starting with any number of bars gives the number of tenths each person receives, i.e. n÷10 = n/10?
- Also generalise the same pattern for halves:
- 2÷2 = 2/2 and 2÷2 = 10/10 = 1.0
- 3÷2 = 3/2 and 3÷2 = 15/15 = 1.5 etc.
- Put the students into small groups of two or three with the following problem:
Are there other numbers of people that the Breakaway Chocolate bar could be shared equally among? Remember that the bar can only be broken along the snap lines.
Are there numbers of people that it could not be shared amongst using the current design? - Ask: What could the people at Breakaway Chocolate do about that?
- Provide the students with scissors and copies of Copymaster 1 to work with. Students may benefit from working in pairs. Rove and watch for the following:
- Do the students realise that factors of ten (1, 2, 5, 10) give the number of equal shares that the bar can be broken into? So five people will get two tenths each.
- Can they record their findings as equations? I.e. 1÷5 = 2/10 and 1÷5 = 2/10 = 0.2
- Can they record their findings as equations using different representations of decimals (e.g. 0.2, 2/10)?
- Do they realise that other numbers of shares are only possible with more snap lines?
- Do they realise that halving halves gives quarter shares? Do they connect quarter shares to decimals, i.e. 1÷4 = 1/4 and 1/4 = 25/100 = 0.25?
- After a suitable period of group work bring the class together to share the key ideas above. After some discussion ask if the Breakaway Block could be improved to cater for different numbers of equal shares. Note that quarter shares cannot be created with the snap lines on the current design. Tell the students that they will need to improve the design tomorrow.
Session Two
- Remind the students that with the bar divided into ten equal parts only two, five and ten equal shares were possible. The restriction caused complaints to the Breakaway Bar Chocolate Company. The managers decided to provide a free calculator with every bar to help their customers to share equally. Type in 1÷5= on a calculator, preferably on an interactive whiteboard or using a data projector. You may wish to support students in estimating the answer through drawing a diagram of a chocolate bar divided into five pieces.
What does the answer tell us about how much chocolate each of the five people should get?
Expect the students to recall that 0.2 means two tenths so each person gets two pieces. You may like to act out breaking up a paper bar to support the students to understand the quantities involved. - Say: let’s see if the calculator can help.
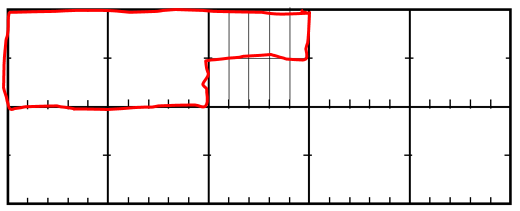
Type in 1 ÷ 4 but do not press the equals sign. Ask the students to predict the answer then confirm to get 0.25. “So how much of a bar is that?” Provide a paper bar partitioned in tenths so students can tell you what they think 0.25 means and looks like. Usually, students suggest this idea for equal partitioning. - We can see that each quarter has two tenths. That explains the 0.2 in the answer but what does the five digit refer to?
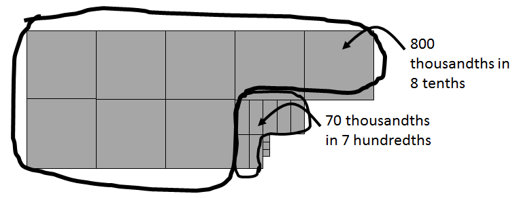
Students might suggest that five means one half of a tenth in the same way ‘point five’ means one half. Ask, “What does the place value chart from yesterday say about the place value of where the five is?” Students should see that the five refers to five hundredths. “But how big is one hundredth on our chocolate bar?” Students may suggest ways to partition the bar but the key idea is that tenths are divided into ten equal parts, as suggested by the arrows on the place value chart. - Highlight that if a tenth is cut into ten equal bits there must be 10 x 10 = 100 of those pieces in one. That is why they are called hundredths. One quarter is made up of two tenths and five hundredths which correspond to the answer of 1÷4 = 0.25.
- Continue the story. “The Breakaway Chocolate Bar Company designed a new bar to go with the free calculator.” Produce the new improved bar (Copymaster 2). Challenge the students, “Is it possible to break this new bar into the numbers of equal shares they claim? For example, how will you divide the bar into eighths, or into thirds? Are other numbers of equal shares possible?”
- Let the students work in groups of two or three to investigate. They will need scissors, copies of Copymaster 2, and a calculator. Encourage the students to experiment with the physical bar first before using the calculator to check their predictions. Look for the following:
- Do they realise that hundredths can also be partitioned into ten equal parts called thousandths?
- Do they realise that the ‘tenth-ing’ could continue infinitely to make smaller and more precise place value units?
- Do they note that thirds are not exactly possible with tenths, hundredths, thousandths, etc. as there is always a unit remaining after the sharing?
- Do they relate the physical model of sharing in place value units to the display from dividing with the calculator?
- Do they realise that if making thirds is problematic then sixths, ninths, twelfths, etc. also results in recurring, non-terminating decimals?
- If some students finish early, challenge them to predict the decimals for sixteenths, thirty-twoths (or one thirty-second), etc. What do they predict will be the decimals for one ninth? one eleventh? one seventh? Bring the class together to discuss the bullet points above. Is the new bar an improvement? Is the claim on the packet correct or misleading?
Session Three
- Begin this session with a matching activity to improve the fluency of students to recognise common fractions and their equivalent decimal representations (see Copymaster 3). Students should work on grouping the words, symbols and decimat models for common fractions. Paper copies are sufficient and students can create a record by gluing the matching cards together on an A3 sized poster. " I have, who has" could be used to extend students.
- After the matching task, ask the students, “Was one fraction different to the others? Why was it different?” Three-quarters was the only non-unit fraction, that is, the only number with a numerator greater than one. Ask, “So how did you decide what the decimal for three quarters is?” The key idea is that non-unit fractions, like three quarters, are formed by joining (iterating) unit fractions. So you might like to record this as:
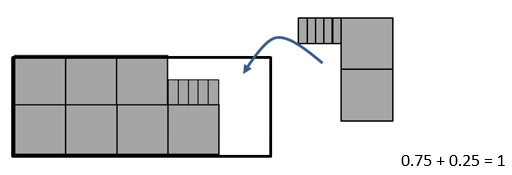
1/4 + 1/4 + 1/4 = 3/4. The decimal equivalent of this is 0.25 + 0.25+ 0.25 = 0.75 - You might also like to show this as three lots of 0.25 made from decimats being joined. An interesting point is “Why is the decimal not zero point six fifteen since 3 x 2 = 6 and 3 x 5 = 15?” Recognising that ten hundredths form another tenth is an important principle that students should transfer from whole numbers, e.g. ten hundreds form one thousand in the same way that ten thousandths form one hundredth. Continue adding 0.25 to your model. Ask the students to predict the new decimal, use a calculator to confirm the result, and invite the students to explain why this happens. Why 0.75 becomes 1 is particularly interesting, especially as many calculators do not display the decimal point. In this scenario ten hundredths are renamed as one tenth and ten tenths are renamed as one.
- Create a sequence of counting in quarters, or sets of 0.25, promoting the link between fractions and decimals as you go. See if students recognise the equivalence, e.g.
- Ask the students to work in groups to find the fraction names for the following decimals.
3.5 0.7 1.8 0.625 2.6 0.873
There are an infinite number of possible fractions for each decimal so tell the students that many answers are possible. Support the students to justify their answers and support their justification with decimat models. Provide paper decimats, scissors and calculators for each small group. - Early finishers can challenge other students by creating their own decimal to fraction task. Look for the following:
- Do the students connect their knowledge of decimals for unit fractions to converting decimals to non-unit fractions? E.g. 0.7 is 7 x 0.1 so it is seven tenths.
- Do the students create appropriate decimat models to justify their answers? E.g. 3.5 should be shown as seven lots of five tenths.
- Do they know that a ‘dot’ over a digits or group of digits indicates infinite recurrence of those digits?
- Do they know that decimal place value also provides a fraction name for decimals? E.g. 0.873 = 873/1000 and 1.8 = 18/10?
- Share the group answers as a class highlighting the important points above. In the case of the last point you may need to use decimat models to show how the decimal place values are ‘nested’ in one another. For example, with 0.873 where are the 873 thousandths located?
Session Four
The aim of this session is to connect addition and subtraction of decimals with the place value understanding students have built up over the previous three lessons.
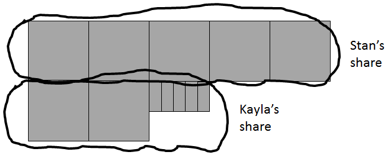
- Begin with the Stan and Kayla story (Copymaster 4) in which two children share three quarters of a Breakaway Bar. What fraction of one bar might each person get?
The simplest answer is for Stan to get one half of a bar and Kayla to get one quarter. Make a decimat model to illustrate that break up beginning with three quarters, 0.75. - Ask how this might be recorded mathematically. Look for various ways to express this partitioning such as:
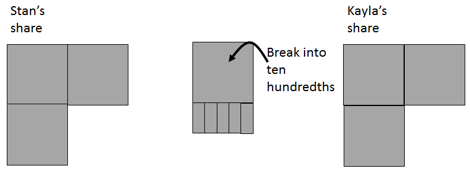
1/2 + 1/4 = 3/4, 0.5 + 0.25 = 0.75, 3/4 - 1/2 = 1/4, 0.75 – 0.5 = 0.25, etc. - Ask, “What would happen if Stan and Kayla had equal shares?” Students may solve this problem using either fractions or decimals or both simultaneously. Consider how 0.75 can be equally shared to get 0.375 + 0.375. A physical decimat model will be very important so students can see how one tenth can be broken into ten hundredths and one hundredth can be broken down into ten thousandths.
Leads to…
Leads to… - Ask students how this partitioning might be recorded:
3/8 + 3/8 = 3/4, 0.375 + 0.375 = 0.75, 3/4 - 3/8 = 3/8, 0.75 – 0.375 = 0.375, etc. - Concentrate on the decimal representations, particularly 0.375 + 0.375. Ask, “Why does the answer (0.75) have only two decimal places when the addends have three decimal places?” Look for students to know that two sets of five thousandths form one hundredth. “If you add three tenths and three tenths you get six tenths. Why does the answer (0.75) have seven in the tenths place?”
- Challenge the students to come up with other fraction and decimal possibilities for Stan and Kayla to share three quarters of a Breakaway Bar. Emphasise the importance of recording the possibilities in multiple ways. Provide the students with copys of the chocolate bar, scissors and calculators. Look for the following:
- Do the students look flexibly at links between fractions and decimals?, e.g. If Stan gets four tenths (0.4) then Kayla must get 0.35 which is three tenths and five hundredths.
- Do they flexibly combine and partition decimal place value units?, e.g. 0.7 (seven tenths) I halved to get 0.35 (three and one half tenths or 35 hundredths).
- Do the students justify their answers using multiple sources of evidence?, e.g. Shares of 0.7 and 0.05 are substantiated using decimal fractions, the calculator, and the decimat model.
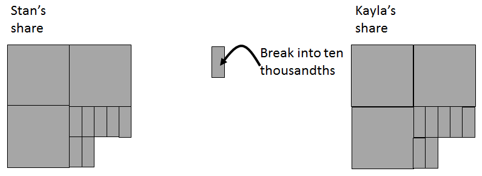
- Do capable students challenge themselves to extend the decimal system beyond thousandths?, e.g. Stan gets 0.4025 and Kayla gets 0.3475.
- After an appropriate period of investigation bring the class together to share answers. Recognise novelty in solutions and risk taking. For example, does any group make Kayla’s share one third which leads to 0.416 and 0.333? Highlight at least one solution where place value units are partitioned or combined.
- As a final individual assessment task ask the students to solve these two decimal calculations:
0.25 + 1.8 = ? 3.52 – 1.9 = ?
Look for students to apply their place value understanding and link fractions with decimals where appropriate. These addition problems could be a good opportunity for students to draw on their cultural backgrounds and daily lives and make the contexts of problems more relevant.
Dear parents and caregivers
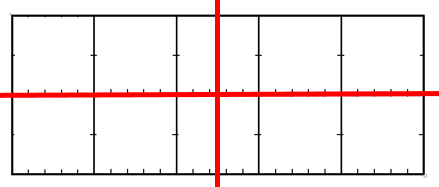
This week we are beginning work on decimals. We will be using a paper model of a Breakway Chocolate Bar. Don’t worry we won’t be eating lots of real chocolate. The simplest chocolate bar is divided into ten equal parts like this:
By snapping the bar along the dark lines, the bar can be shared equally among two, five or ten people. The shares can be written as decimals and fractions, e.g. one fifth is two tenths or 0.2. This model will help us to explore the relationships between simple fractions and decimals. By the end of the week we may even be adding and subtracting decimals.