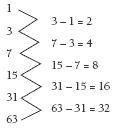This is a level 3 algebra strand activity from the Figure It Out series.
A PDF of the student activity is included.
Click on the image to enlarge it. Click again to close. Download PDF (310 KB)
use a table to find and predict patterns
FIO, Level 3-4, Algebra, Bits and Pieces, page 5
ruler, stapler, scissors
Activity One
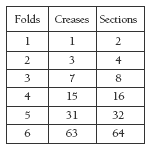
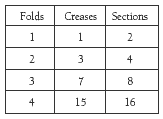
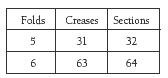
Most people find visualising the number of creases and sections very difficult. Give the students paper to fold to check their predictions and to complete the table. There are several interesting patterns in the table.
The creases and sections columns share the same pattern, based on subtraction. Here is the pattern for the creases column:
Note that the differences shown in the creases pattern are the figures found in the sections column.
The students are most likely to notice that each extra fold doubles the number of sections and that there is one less crease than there are sections:
These rules are recursive rules rather than functional ones. Note that with recursive rules, you cannot find the nth number in a pattern unless you know the previous number.
There are also functional rules that link the number of folds with the numbers of creases and sections. These rules use exponents. The number of sections doubles with each fold. So three folds will give 2 x 2 x 2 (or 23) = 8 sections. If f is the number of folds, s is the number of sections, and c is the number
of creases, then:
s = 2f
c = 2f – 1
With this functional rule, you can now find any number in the pattern. (You don’t have to find the previous number.)
Students at levels 3 and 4 are not expected to be able to put together functional rules such as these.
Activity Two
To clarify any confusion, you may need to point out to the students that one sheet of paper is two pages. In terms of the activity, they need to know that the number of folds includes the folds that are later cut. The comments and rules below are based on the first cut being the second fold.
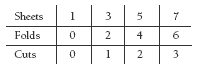
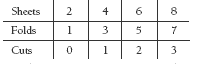
Question 1 concentrates on odd numbers of sheets. The students could experiment with small numbers of odd sheets and put their results in a table:
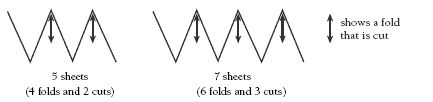
Diagrammatically, this can be shown as:
The table shows that the number of folds for odd numbers of sheets is always one less than the number of sheets. A staple is put through half of the folds to make a spine, so the number of cuts is half the number of folds. So the rule for odd numbers of sheets is: folds = number of sheets – 1 and cuts = number of folds ÷ 2. This could be expressed, as in the Answers, as: f = s – 1; c = f ÷ 2, where s is an odd number.
To answer question 2, the students will need to include even numbers of sheets. For even numbers of sheets, the table is:
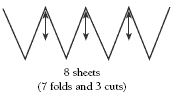
Although the number of folds is still one less than the number of sheets, the rule for cuts is the number of sheets divided by two minus one. For example, for eight sheets, 8 (sheets) ÷ 2 = 4 – 1 = 3 (cuts). As a diagram, this could be represented as:
The rule for this can be expressed as (number of sheets ÷ 2) – 1.
Answers to Activities
Activity One
1. Practical activity. It will have three creases and four sections.
2. a.
b. Pattern: add the creases and sections of each number of folds to get the next
number of creases. For example, 1 + 2 = 3, 3 + 4 = 7.
Activity Two
1. a. 16 folds and 8 cuts
b. 24 folds and 12 cuts
2. Two rules are needed, one for an odd number of sheets and one for an even number of sheets. For an odd number of sheets, the number of sheets – 1 = folds; folds ÷ 2 = cuts. The rule could be expressed as: (f = s – 1; c = f ÷ 2), where s is an odd number. For even numbers, the folds are found the same way, but the number of cuts is half the number of sheets minus one. The rule could be expressed as:
(f = s – 1; c = s ÷ 2 – 1), where s is an even number.