These are level 3 number and geometry problems from the Figure It Out series.
A PDF of the student activity is included.
Click on the image to enlarge it. Click again to close. Download PDF (326 KB)
find fractions of whole numbers (Problem 1)
interpret three dimensional drawings (Problem 2)
solve puzzles related to three dimensional shapes
Problem One
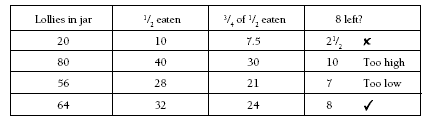
This problem is ideal for using a number of different strategies in combination. For example, consider a trial and improvement, working backwards, table strategy. Students may realise, perhaps through trial and error, that only multiples of eight in the first column give a whole number in the last column.
This could be recorded in an equation like this:
(? ÷ 2) ÷ 4 = 8
Students may use an undoing (opposite) operation to solve it:
(? ÷ 2) ÷ 4 = 8 so ? ÷ 2 = 8 x 4
so ? = 32 x 2
so ? = 64
Writing equations is not a natural method for most students. If students do use the strategy, it is worth encouraging them because it demonstrates that they have a useful understanding of algebraic ideas.
Problem Two
Although students may prefer to build each model using multilink cubes, ask them as a first step to try to recognise the matching models. They can identify the characteristics of a shape and look for a matching model.
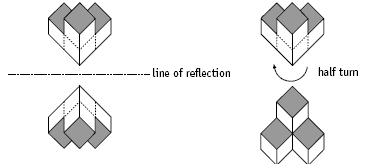
For example, a is an L shape with one arm of three cubes and the other of two cubes. Shape g has similar characteristics. The top view of shape b can be represented like this
, where the number shows the number of cubes in each column. Shape h has the same representation as b if it is turned a quarter turn anticlockwise. Similarly, c can be represented as
, which is a quarter turn anticlockwise of shape e. This leaves shape d as the same as shape f. Notice that d and f are reflections or half turns of each other:
Problem Three
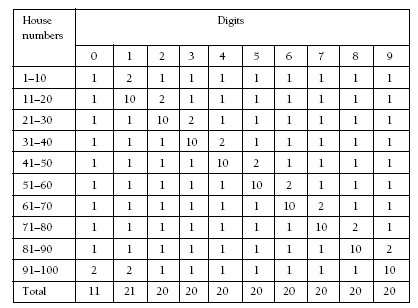
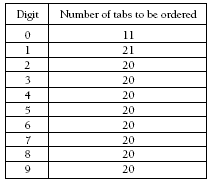
Students may find it helpful to use a hundreds board. Encourage them to work systematically to make their counting more efficient. They could use a table.
Patterns within the table allow it to be completed easily. Students can check they have completed the table correctly by finding out how many digits are needed in total. There are nine single-digit numbers, 90 two-digit numbers, and one three-digit number.
This gives a total of (9 x 1) + (90 x 2) + 3 = 192.
Problem Four
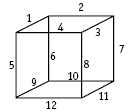
a. A cube has 12 edges. Each edge is 1 metre long, so Priscilla needs 12 metres of pipe.
b. The cube will need a join at each corner (vertex). Since a cube has eight vertices, it will have eight joins.
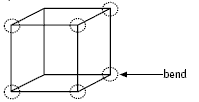
The number of bends depends on how many lengths of plastic tubing are used. If all 12 edges are cut separately, there are no bends. If six lengths are cut, the cube can be made in the following way:
As an extension, you could ask students to work out the minimum number of lengths needed to make a cube. The answer is four. The cube can be made in this way:
In this case, eight bends are needed.
Answers to Problems
1. 64 lollies
2. a and g, b and h, c and e, d and f
3.
4. a. 12 metres
b. The minimum number of bends is 6 (if 6 lengths of plastic piping are cut) and the
minimum number of joins is 8.