The unit involves students in solving problems that can be modeled with algebraic equations or expressions. Students are required to describe patterns and relationships using letters to represent variables.
- Predict further members in patterns of equations using relationships within the equations.
- Develop function rules to describe relationships.
- Find specific values for variables from given relationships.
Algebraic thinking is about generalisation, describing something that consistently occurs in a particular situation. In algebra, letters are used to express generalisations. Einstein’s famous equation e=mc2 expressed a relationship about the amount of energy, the mass of matter, and the speed of light.
Letters may be used to express an important number. In Einstein’s equation c represents the speed of light, a number. Letters can also refer to a specific unknown. For example, “Mere gathers some pipi. Rawiri gives her seven more pipi. Now she has 18 pipi in her bucket.” x + 7 = 18 expresses the unknown number of pipi she first collected.
Letters are used more powerfully to express generalised relationships as Einstein did. The equation v=d/t expressed velocity as a function of distance divided by time. All of the letters refer to variables, quantities that can change relative to each other.
Algebra is loaded with conventions about how unknown variables are expressed. For example, 5x refers to x multiplied by five, t2 refers to t multiplied by itself, and n/m refers to the division of n by m. Decoding algebra is similar to learning to read. Students need lots of experience linking symbols with the meaning of those symbols.
Students can be supported through the learning opportunities in this unit by differentiating the nature and complexity of the tasks, and by adapting the contexts. Ways to support students include:
- providing a physical model, cups and cubes, so students can represent relationships and think with those relationships
- modeling how to record relationships as diagrams, and capture adjustments to the models. Flowcharts are very useful in supporting students to organise the order of inverse operations
- explicitly telling students about the conventions of letter symbols, e.g. 5x means five times an unknown x, with a ‘missing’ multiplication sign
- encouraging students to work collaboratively and share their ideas
- encouraging students to check their solutions against the conditions of the problem.
Tasks can be varied in many ways including:
- altering the complexity of the patterns and relationships that are used. The unit gives a variety of problems that can be adapted to change difficulty
- varying the number of steps in a problem and the difficulty of calculating the result of those steps
- providing or removing examples of a pattern or relationship before trying to generalise the relationship using variables.
This unit is focussed on learning how to use algebraic expressions and equations, and the teaching sessions are not set in a real world context. You may wish to explore real world applications of algebra in the teaching sessions following the unit, for example bags of ingredients going into a manufacturing machine, servings of food at a hāngī, or ticket prices for an event.
- 5 x Large regular plastic bottles (2L fruit juice or 1L milk bottles are good)
- Opaque plastic cups of different - red, yellow and blue are referred to below
- Cubes – multilink, unifix, etc.
- Copymaster 1
- Copymaster 2
Session 1
Make up a set of three containers by trimming down 1.5 litre plastic soft drink bottles. It is preferable that these containers are of the same type. Straight-sided bottles are better than curved ones as they make it easier for the students to predict the relationships. The three cut down containers should hold different amounts of water when full. Make their capacity no more than 500 ml and ensure that these capacities are not multiples of each other, e.g. 120 ml, 230 ml, and 400 ml would be better than 100 ml, 200 ml, and 400 ml. Label the containers p, q, and r respectively.
- Introduce the containers to the class and use them to set representation problems for the students by pouring from the p, q, and r containers into the large container, preferably the original bottle type that p, q, and r were created from.
With each problem students write an expression for the water level. Here are some examples. You can extend these as appropriate for your class.- Pour one lot of p and one lot of r into the big bottle:
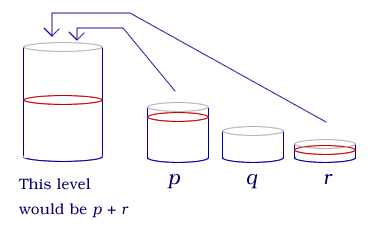
- Pour two lots of p, one lot of q and one lot of r into the big bottle:
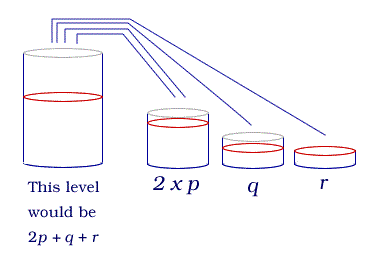
- Pour four lots of p into the big bottle.
How can you write an expression for what is in the bottle? (p + p + p + p or 4p, noting that 4p has an ‘assumed’ multiplication sign, 4 x p)
Next pour from the bottle into container r and container q until the mark is reached.
What is left in the bottle? How might you write an expression for that amount? (This gives 4p – r – q which can also be written as 4p – (r + q))
- Pour five lots of r into the large bottle (5r).
Pour out two lots of p (5r – 2p).
- Pour three lots of r and three lots of q into the large bottle (3r + 3q or 3(p + q))
Pour out two lots of p.
(This gives 3r + 3q – 2p which could be written as 3(r + q) – 2p).
- Pour two lots of r and one lot of p into the large bottle (2r + p)
Repeat pouring 1, that is add two lots of r and one lot of p into the large bottle
(2r + p + 2r + p, or 2(2r + p) or 4r + 2)
- Pour one lot of p and one lot of r into the big bottle:
- Change the activity from representing pouring with an expression to imaging the pouring that matches a given expression:
- What does p + q – r mean? What pouring happens?
- What does 3r + q – 2p mean? What pouring happens?
- What does 3(p + q) mean? What pouring happens? (Put p + q in the bottle. Do that three times.)
- What does 3(r + q) – 2p mean in terms of pouring? (Put r and q lots together 3 times and then pour out p twice.)
- Pose problems that give opportunities for students to discover equality or inequality of expressions. You will need two identical bottles to pour into.
Are these expressions equal or unequal? Why?- q + 2p and p + 2q (only equal if p and q are equal)
- q – r + p and p + q – r (yes they are equal)
- 3r + 2p and 3p + 2r (only equal if p and r are equal)
- Explore equality of expressions, particularly in the cases where order does or does not make a difference to the result, e.g. 2r + p = p + 2r = r + p + r.
Can students simplify the equality using inverse operations?
p + 2r = r + p + r
2r = r + r (subtracting p from both sides)
- Provide students with applications of equality and inverse operations.
Which of these are correct and which are false? Explain your answers.- 4(r + q) = 4r + 4q (equal)
- 3(r + q) – 2p = q + r + 2(r – p) + 2q (equal)
- 4p – r – q = p + 2(p – r – q) + q + r + p (equal)
- 2r + p + q = 2(p + q) + 3r – q – p – 2r (unequal)
Students could make up their own set of containers, label them with algebraic letters, and develop challenges for each other. Alternatively, the class containers could be left as a station for students to use independently.
Session 2
In this session students look for patterns within each equation set and use these patterns to predict further equations in the set. They may do this using recursion, that is finding a relation between consecutive equations, rather than by looking for relationships within the equations across the equals sign. Highlight relationships that might be found between the numbers in each set of equations and encourage the students to look for ways to describe these relationships. It is important that students find the unknowns using mental calculation rather than with calculators, as their attention needs to be on the relative size of numbers.
Some learners will need support from physical materials to notice and describe the patterns. Connecting cubes in stacks make a useful representation.
Below are some suitable equation patterns:
- 1 – [ ]= 1
2 – [ ] = 1
3 – [ ] = 1
4 – [ ] = 1
...
456 – [ ] = 1
Why is the right-hand side of the equation always one?
What is the rule for all equations in this pattern?
Use this pattern to solve:
2000 – [ ] = 1
1001 – [ ] = 2
- 0 + 1 + 2 = [ ]
1 + 2 + 3 = [ ]
2 + 3 + 4 = [ ]
3 + 4 + 5 = [ ]
Is there anything in common with the numbers in the boxes?
Why do you think this happens? (The number in the [ ] is three times the middle number on the left-side of the equation.)
a + b + c = 300 , a, b and c are different numbers.
What numbers could they be?
What values for a, b and c would fit the pattern?
A physical representation of the pattern, using connecting cubes, would look like this: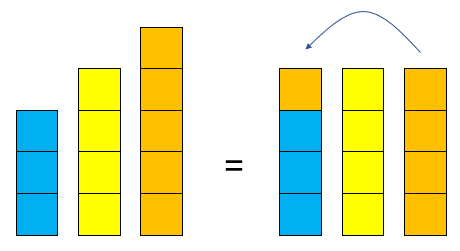
- 42 – 8 = [ ] – 10
52 – 8 = [ ] – 10
62 – 8 = [ ] – 10
...
92 – 8 = [ ] – 10
712 – 8 = [ ] – 10
What rule can you find for equations in this pattern?
- 1 x 9 + 1 = [ ]
2 x 9 + 2 = [ ]
3 x 9 + 3 = [ ]
4 x 9 + 4 = [ ]
...
In [ ] x 9 + [ ] = 100, what is [ ] if both [ ] are the same number?
What rule can you find for all the equations in this pattern?
A physical model of this pattern, made with cube towers, looks like this
(example of 4 x 9 + 4 = 40 (4 x 10)):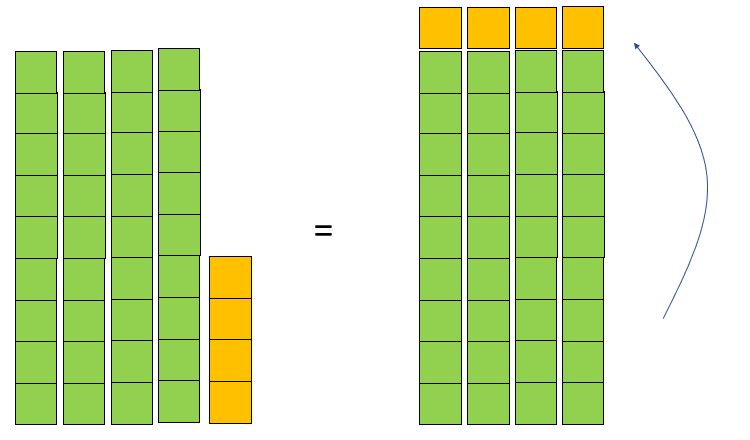
- 1 = [ ] ÷ 11
2 = [ ] ÷ 11
3 = [ ] ÷ 11
4 = [ ] ÷ 11
...
In [ ] ÷ 11 = 7, what is [ ]?
In 9 = [ ] ÷ 11, what is [ ]?
What rule can you find for equations in this pattern?
Would these equations be further down in the pattern?
Give an explanation. [ ] = 121 ÷ 11
[ ] = 594 ÷ 11
[ ] = 682 ÷ 11
Session 3
Students solve “What’s my Number?” problems and record how they found the final answer. At this stage trial and improvement are legitimate strategies though the problems encourage students to attend to structure, and apply their understanding of inverse operations.
Flowcharts can support students to apply inverse operations. Consider the problem; “Take my number, multiply it by three then subtract 4. The answer is 20. What is my number?” The problem is equivalent to 3x - 4 = 20.
A flowchart looks like this:
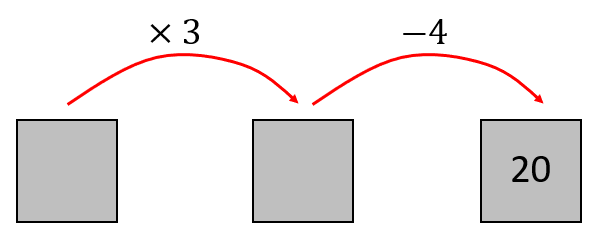
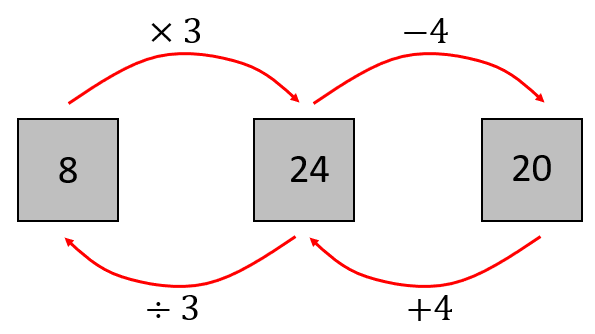
Applying inverse operations gives:
- If you take my number, multiply it by three then add seven, you get fifty-two.
What is my number?
(15 since 15 x 3 + 7 = 52, or 3 x [ ] + 7 = 52, so 3 x [ ] = 45, and [ ] = 15)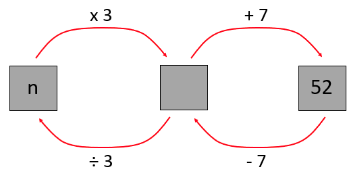
- If you take my number, subtract ten from it then divide it by two, you get sixteen.
What is my number?
(42 since 16 x 2 = 32 and 32 + 10 = 42)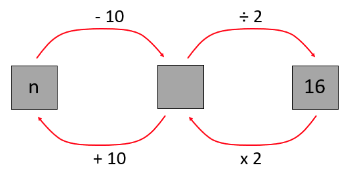
- If you take my number and add twenty-four to it, the answer is three times my number.
What is my number?
([ ] + 24 = 3 x [ ], so 24 = 2 x [ ], and [ ] = 12)
- If you take my number and divide it by three, the answer is the same as my number minus forty.
What is my number?
([ ] ÷ 3 = [ ] - 40, so 40 = 2 x [ ], and [ ] = 60)
- If you take my number and multiply it by itself, the answer is my number added to itself.
What is my number?
(2 since 2 x 2 = 4 and 2 + 2 = 4 and 0 for the same reason;
or [ ] x [ ] = [ ] + [ ], so [ ] x [ ] = 2 x [ ] , and [ ] = 0 or [ ] = 2.)
- Ask students to make up “What’s my number?” problems for others to solve. They should provide hints to other students about solving the problem. For example, “My number is multiplied by six. How do you undo multiplying by six?”
Session 4
In this session students work out the functional rule for given input and output numbers. The functions increase in complexity as the week progresses. Each example offers the students three input/output pairs. to the right of these three pairs are three other pairs (typed in bold) that could be used if needed. Copymaster 1 can be used to make stimulus cards by cutting and folding the output of the three additional pairs behind so they can not be seen unless needed.
The rule is two times the input number less one gives the output number.
The rule is times three plus one.
The rule is times three take away nine.
The rule is divide by two plus one.
The rule is the input number multiplied by itself (squared).
Discuss how a rule might be found.
If the output numbers are always more than the input numbers what types of rules do you try first?
Students are likely to suggest addition or multiplication. That strategy is useful but needs to be qualified. Multiplying by a fraction less than one or an integer will result in smaller output numbers.
How can you check if only addition is involved?
The difference between input and output numbers must be constant. That generalisation is true of subtraction as well.
How can we check if only multiplication is involved?
The differences between input and output numbers change. That will not work as a strategy. Students will need to estimate what the multiplier is, possibly from two pairs, then check to see if the multiplier applies to the other pairs.
If division is in the rule, how can you tell?
Students usually say that division, like subtraction, makes the output number smaller. That generalisation is naïve since division with a fraction between zero and one makes the output number larger. However, provided the divisor is larger than one the claim that “division makes smaller” holds. As with multiplication, the divisor will need to be estimated first then tried on the input-output pairs.
Challenge students to come up with their own tables of values. You might set up a spreadsheet of tables as a template, with hidden rules. Alternatively create a paper template as seen in Copymaster 1.
Session 5
These activities involve students in working out the number of counters or cubes that are in each cup of a given colour. Several clues are provided, and students must combine these clues to find a solution. Use opaque coloured plastic cups, that are readily available in supermarkets, warehouses, and dollar stores. For each problem all students should solve it, then record their reasoning, before the solution is “revealed.”
Encourage students to check their solutions by putting the values they assign to each cup back into the original clues. Do all the clues work? If not, try again!
Examples of cups and counters problems follow. The first sentence is the instruction for the teacher and gives the answer. It does not appear on (Copymaster 2) as students use the clues to work out how many cubes are in each coloured cup.
- Into each yellow cup put four cubes, into each blue cup put five cubes.
Clues:
14 cubes in total 16 cubes in total
- Into each yellow cup put three cubes, into each blue cup put six cubes.
Clues:
Four yellow cups have the same number of cubes as two blue cups.
Three yellow cups and one blue cup have 15 cubes in total.
- Into each yellow cup put five cubes, into each blue cup put three cubes.
Clues:
Three yellow cups have the same number of cubes as five blue cups.
One yellow cup and two blue cups have 11 cubes in total
- Into each yellow cup put two cubes, into each blue cup put four cubes, and into each red cup put six cubes.
Clues:
Six yellow cups have the same number of cubes as three blue cubes that have the same number of cubes as two red cups.
Two blue cups and one red cup have 14 cubes in total
- Into each yellow cup put seven cubes, into each red cup put seven cubes, and into each blue cup put five cubes.
Clues:
Five yellow cups have the same number of cubes as seven blue cups.
Five red cups have the same number of cubes as seven blue cups.
One red cup and one blue cup contain 12 cubes.
Is there more than one possible answer? (y = 6, r = 6, b = 6 also works)
Dear parents and whānau,
This week we have been looking at equations with unknowns. We are learning to express relationships using the language of algebra, particularly using letters to represent amounts that we do not know.
Try the following with your child:
Write 8 on a small piece of paper and 4 on another piece. Hold the numbers in different hands so that your student can’t see them. Say, “One number is twice the other, and both numbers add to 12. What numbers are in my hands.”
Get your child to make a problem like this for you. He or she might share the problems they are solving in class.
Enjoy challenging each other!