These are level 3 algebra, geometry and number problems from the Figure It Out series.
A PDF of the student activity is included.
Click on the image to enlarge it. Click again to close. Download PDF (295 KB)
explore patterns (Problem 1)
solve problems involving transformations (Problem 2)
use addition skills to solve problems relating to distances (Problem 3)
solve problems using addition (Problem 4)
Problem One
Encourage the students to experiment with cards and to try to solve a smaller case before you go over this method with them.
To get the cards 1, 2, 3, 4, and 5 in the right order, you have to start off with the order 1, , 2, O, 3, ♣, 4, ♠, 5, ♦, where the symbols stand for an unknown card.
The has to be 6 because Derek will have put the ♦ on the bottom of the pile and the will be dealt next. This tells you that the original order is 1, 6, 2, O, 3, ♣, 4, ♠, 5, ♦. It’s tempting to think that the O in this revised line up is 7. But that O goes on the bottom of the pack. So it’s the ♣ that is 7. The original order is now 1, 6, 2, O, 3, 7, 4, ♠, 5, ♦.
The ♠ goes on the bottom of the pack, and so the ♦ must be 8. This gives 1, 6, 2, O, 3, 7, 4, ♠, 5, 8.
The O has to be missed again because it is put on the bottom of the pack. So the ♠ is 9. The O has to be 10. The original order is therefore 1, 6, 2, 10, 3, 7, 4, 9, 5, 8.
The students can check this with a pack of 10 cards.
Discuss other methods that the students come up with for solving the problem. For example, they may put 10 cards in order from 1 to 10, deal them out in the order Derek did, and then work backwards from the way the cards were dealt to get the original order.
Extension
“What if Derek had had 20 cards to start with? What order would they have been in? Can you do 50?”
Problem Two
This could be a good problem to include in a unit of work about books, including how books are written and edited, the history of printing, current printing technology, and book design.
The students will need some understanding of how sheets of paper are folded and cut to make up books. They will probably have made their own books in which they’ve put several pages on top of each other, stapled them down the middle, and folded the pages over the staples. They could experiment by making books like this and seeing where the page numbers are positioned when the pages are unstapled.
This is a difficult problem to visualise. Model it by folding an A4 piece of paper in half twice, cutting most of the way across the fold (which is at the top or the bottom, depending on how you folded it), and numbering the pages in order. (Cutting most of the way and leaving a bit of the pages still attached means you can open the paper up again and see where the page numbers are positioned.) The position of the page numbers will vary depending on whether your fold was at the top of the page or the bottom of the page.
Problem Three
There aren’t many possible routes in this problem, so trying all possible routes is still an efficient strategy. You could begin by asking the students what they think will be the shortest route.
The 9 kilometre road from Nìkau to Kòwhai is the longest leg in the journey, and students may try to find a way to avoid travelling this road. They will find, though, that if they avoid it, they will have to travel another road twice, which will make the overall journey longer.
Whichever route the students choose, there is only one road going through Wainui. So they could start with Paki, 7 kilometres, Wainui, 5 kilometres, Te Poi. At this point, they either go to Nìkau or Kowhai. The first way gives Paki, 7 kilometres, Wainui, 5 kilometres, Te Poi, 3 kilometres, Nìkau, 9 kilometres, Kowhai, 5 kilometres, Paki, a round-trip distance of 29 kilometres. Or the second way is Paki, 7 kilometres, Wainui, 5 kilometres, Te Poi, 5 kilometres, Kowhai, 9 kilometres, Nìkau, 5 kilometres, Paki, a round-trip distance of 31 kilometres. The students should realise that it would be shorter overall to use the 3 kilometre trip between Te Poi and Nìkau.
Problem Four
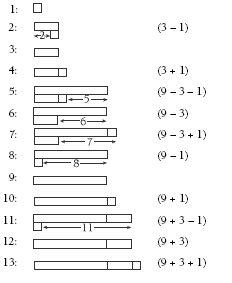
This looks a lot like Problem One, page 3. How can you get all the numbers from 1 to 13 using 1, 3, and 9 and addition and subtraction?
The answers show how you can find all the numbers. In the equations, + essentially means put the sticks end to end and – means put as a second row and use the difference between the lengths of the two rows.
Hints for Students
1. Try a smaller case first and try using equipment.
2. Answers will vary depending how the paper is folded and cut.
You could check your work by putting page numbers on a piece of paper, folding it into a book, stapling and cutting the pages, and cheking that the page numbers are in the right order.
3. Find all possible round trips – there aren’t that many.
4. This problem is really about numbers. See Problem Three, page 3.
Answers to Problems
1. 1, 6, 2, 10, 3, 7, 4, 9, 5, 8
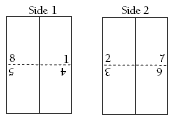
2. With the cut made at the bottom:
3. a. There are essentially only two routes, but you can go either forward or backward in the cycle. If you started at Paki, the two routes would be: Paki, Wainui, Te Poi, Nìkau, Kowhai, Paki or Paki, Wainui, Te Poi, Kowhai, Nìkau, Paki.
b. The first route given in a is the shortest, at 29 km. (The second route is 31 km.)
4. Answers will vary. Some ways are: