The purpose of this activity is to engage students in an investigation of the area of circles.
This activity assumes the students have experience in the following areas:
- Perimeters of polygons and the circumference as perimeter of a circle.
- Areas of simple polygons.
- Metric units for length and area, with standard notation, e.g., 36 cm2.
The problem is sufficiently open ended to allow the students freedom of choice in their approach. It may be scaffolded with guidance that leads to a solution, and/or the students might be given the opportunity to solve the problem independently.
The example responses at the end of the resource give an indication of the kind of response to expect from students who approach the problem in particular ways.
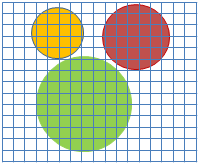
Task: Find the area of one of these circles and use this to establish a general rule for any circle of radius r.
The following prompts illustrate how this activity can be structured around the phases of the Mathematics Investigation Cycle.
Make sense
Introduce the problem. Allow students time to read it and discuss in pairs or small groups.
- What are the important words and symbols? (The meaning of ‘general rule’ as applying to the area of any circle is important.)
- Can I imagine (visualise) what the numbers or shapes look like? (How might a student partition a circle into shapes that are familiar?)
- Does this look/sound like a problem I have worked on before? (What other shapes can I find the area for? Do I have a general rule for the area of these shapes?)
- What information has been given? (How might a student find the areas of the given circles?)
Plan approach
Discuss ideas about how to solve the problem. Emphasise that, in the planning phase, you want students to say how they would solve the problem, not to actually solve it.
- What are the maths skills I need to work this out?
- What could the solution be? (A general rule should use a known measurement of the circle to find the area? What might the known measurement be?)
- What else do I need to know to get started?
- What strategies can I use to get started?
- Can I notice a pattern to write down and explore? (Collating data from the three given circles in a table may help students to identify relationships.)
- What tools (digital or physical) could help my investigation?
Take action
Allow students time to work through their strategy and find a solution to the problem.
- Have I shown my workings in a step-by-step way? (Students need to clearly show how they found the areas of the given circles. They also need to show how they chose to partition a circle of any size.)
- How can we share the mahi in our group to get the best result? (Getting more data about the areas of other sized circles might make it easier to see a relationship between radius and area.)
- How can we stay connected?
- Does my general rule seem correct? Have I checked it with lots of example of circles?
- Can I prove my general rule works for any circle? (Students might prove the area formula geometrically.)
Convince yourself and others
Allow students time to check their answers and then either have them pair share with other groups or ask for volunteers to share their solution with the class.
- What is the general rule?
- Show and explain how you worked out your general rule.
- What connections can I see to other situations, why would this be? (For example, the general rule might work for ellipses if it is altered.)
- Have I tested my generalisation out on other cases (e.g., Circles of many different sizes.)
- How can I clearly show what I found out?
- Which ideas would convince others that my general rule works?
Examples of work
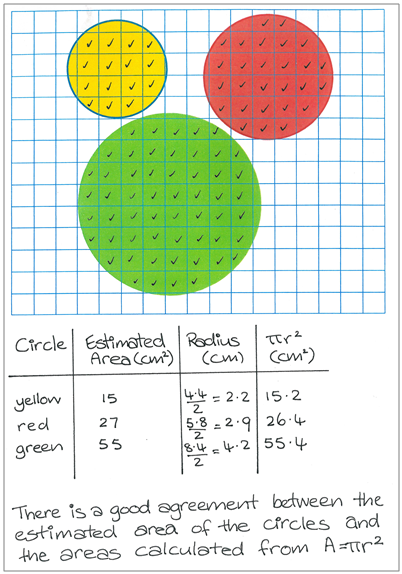
The arithmetic approach
The student carries out directed calculations that will lead them to verify the formula for the area of a circle.
Click on the image to enlarge it. Click again to close.
Work sample 2
The student carries out an algebraic investigation that would allow them to verify and to show, by example, the derivation of the area of a circle formula.
Click on the image to enlarge it. Click again to close.
Work sample 3
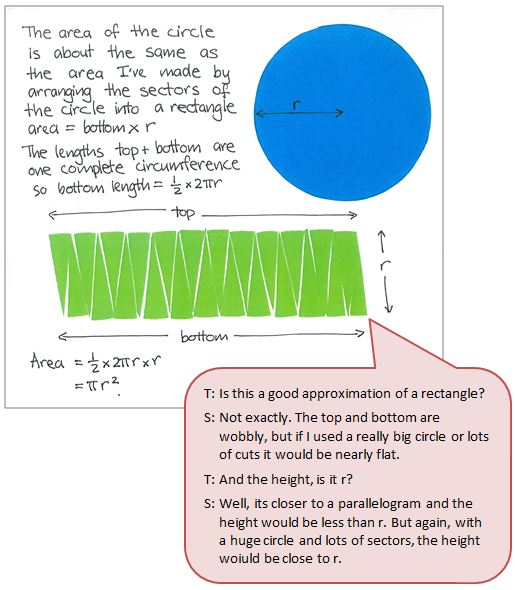
The student develops a generalised rule, by partitioning a circle of any size and relating area to radius.