Archery Addition

Some students in year 7 and 8 classes solve problems like these using only counting strategies. Many others use a ritualistic memorisation of the vertical working form (algorithm). Although they can find the correct answer, they may have missed the opportunity to develop the true additive thinking strategies that are vital to their mathematical development.
These thinking strategies are modelled in the diagrams and speech bubbles in this activity. They are examples of the ways in which students can use their knowledge of number relationships to find easy and efficient ways of calculating.
Avoid instructing your students to simply copy these ways of thinking because this would result in them trying to memorise another “way” of doing the sum. Encourage them to think about different ways of solving the problems, as illustrated by Toline and Michael, and ensure that they can communicate their understanding of these through their discussion and use of diagrams. The strategies that the students then use for themselves become a matter of personal choice, a choice that is based on knowledge and understanding.
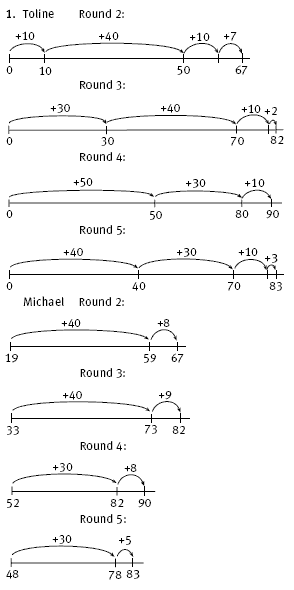
Toline is modelling what is called “front-end addition” because she is starting at the front by adding the tens. This is a very common mental strategy among adults, despite their being taught to start from the ones place at school. Try extending the use of Toline’s method to add three- and four-digit numbers.
Michael’s method extends the counting-on idea by starting from a quantity, breaking up the other addend into useable parts, and then adding on those parts. You can extend this idea by trying to use it to join three or more addends.
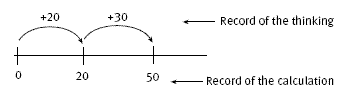
The open number lines record both the thinking and the calculation in a way that reflects what the student is doing. Unlike a traditional number line, the spaces do not have to be separated in the correct proportion to match the quantities; it is more a schematic drawing of the thinking steps.

Answers to Activity

1.

2. 37