In this unit, students will learn to investigate polygons using an instrument of their own construction. They should be able to find the general formula for the number of degrees in any polygon (including a triangle). Finally they will investigate an interesting locus problem related to polygons.
- Make an instrument to measure turning in a range of situations.
- Measure angles using the new instrument.
- Investigate angles of polygons.
- Find counter-examples to incorrect conjectures.
Many students rely on the memory of geometrical results and not on fuller understanding of these results. This unit is an introduction to a number of important geometrical ideas. But the emphasis is on the students developing skills that will enable them to develop a deeper understanding of the results in question.
In the process they should be encouraged to find geometrical results of their own and to justify the truth of these results. They should also be able to find counter-examples if their conjectures are wrong.
The above is at the heart of mathematics. It is important to find things and be able to use them but it is also important to show that what you have found is indeed true for a whole class of objects.
Session 1
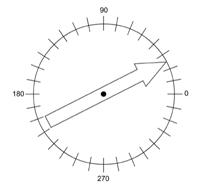
In this session (or in an introductory session) the students make the piece of equipment called a Turn Measurer (TM) and begin to use it for measuring amounts of turn.
Both the circle and the arrow need to be made of clear plastic. The sort of stiff plastic used used in packaging works well. The circle is calibrated with the angles from 0º to 360º in steps of 10º. The arrow needs to be able to rotate about its centre. A flat backed drawing pin (pointing upwards) could be used as the centre pin. The circle should be approximately 6cm in diameter.
-
Give each of the students time to make their own TM. This session is likely to appear somewhat pointless to the students. They will need to trust you that this piece of equipment, and more importantly, the mathematical idea it helps us understand, is of particular importance, and it will eventually make some otherwise difficult ideas easy.
-
Once the equipment is made the students need to learn how it can be used to measure the sum of two or more turns. Issue each student with a piece of paper with 3 rays. Any values of s and t could be used.
.jpg)
-
Initially the students should place the TM with the centre on C and the arrow (set to 0º) pointing to A. The students now turn the arrow so that it points to B.
How far did it turn? -
Now continue the turn by turning the arrow to point to D. They can read the total turn from the TM. Repeat this little exercise until the students understand how the TM can be used to sum 2 or more turns.
-
Now move to a new type of example.
.jpg)
-
Set the TM to 0º and place the centre at B with the arrow pointing to A. The students turn the arrow until it points towards C (through the angle marked s). Now they slide the TM along the line BC until the centre is at C. The arrow should still be pointing along the line from C to D. Now they turn the arrow until it points towards E.
What is the total turn? -
This basically boils down to a turn of sº minus tº. For example, if s is 60º and t is 50º the TM should be showing a total turn of 10º. Try other similar examples until the students are confident with this situation.
-
Now try examples such as the one below.
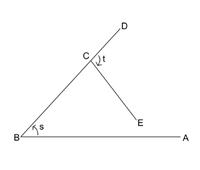
-
Here the total amount of turn will be negative. For instance, if s is 60º and t is 110º the total turn will be -50º.
[Of course, the TM will actually show 310º. However, students should not have difficulty viewing this as -50º. Alternatively, the TM could be dually calibrated from the start with negative values running clockwise.] -
Now try examples such as the one below.
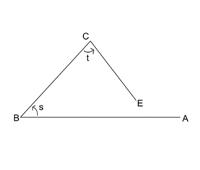
-
In this case the students should set the TM to 0º with the arrow pointing to A, and with the centre at B. They then turn the arrow through the angle s. Slide the TM until the centre is at C, and turn the arrow through the angle t. You will see that in this case they are turning the back half of the arrow through the angle t. What is the total turn? If s is 60º and t is 70º the total turn will be 130º.
-
Now try the diagrams below. In the first case if p is 60º, q is 90º, and r is 50º, the total turn will be 20º. In the second case, if p is 60º, q is 290º, and r is 50º, the total turn will be 400º.
.jpg)
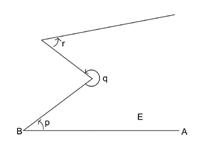
-
Examples such as the second one above may cause problems for the students. Encourage them to do the turns slowly and watch the arrow complete the turns. Encourage them to watch the arrow pass through 90º (if AB is horizontal the arrow will be pointing straight up at this moment). Watch it pass through 180º (at this moment the arrow will be pointing horizontally but right to left). Watch it pass through 270º (straight down), then 360º (horizontally left to right) – the completed turn. This ‘watching’ the whole turn pass through its various key stages is very important.
Session 2
In this session the students’ newly found skill in finding the sum of turns can be put to use to do some valuable mathematics. In particular, we look at the relative sizes of the angles on parallel lines and the sum of the angles of a triangle.
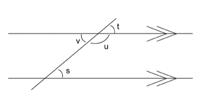
-
On the diagram above get them to carefully explain, using the arrow,
(i) why s and t are the same,
(ii) why s + u is 180º (a straight angle),
(iii)why s and v are the same,
(iv)why v + u is a straight angle.
-
Take time over this. Ensure that the explanations are careful and logical and that they are couched in terms of amounts of turn and in relation to the beginning and end formations of the arrow.
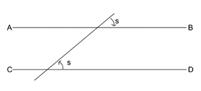
-
On the diagram above get them to carefully explain, using the arrow, why AB and CD must be parallel. Again, take time over this and ensure the explanations are rigorous.
-
Take plenty of time over the next mathematical problem. It has great historical importance and is central in geometry.
-
Activity: Using the arrow, carefully explain why the interior angles in any triangle must always sum to a straight angle.
It is likely that the students will come up with one or other of the following explanations.
Solution 1 involves something like this:
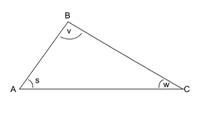
On the diagram above centre the arrow at A pointing left to right; rotate the arrow through s; translate the centre to B; turn through v; translate the centre to C; turn through w; observe that the total turn must be a straight angle.
Solution 2 involves something like this.
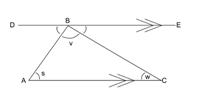
Take any triangle ABC (see above). Draw a line DE that is (i) parallel to AC and (ii) passing through B. Using the arrow it can be seen that the angle DBA must be s, and the angle EBC must be w. Thus, at the point B we have the 3 angles s, v and w which together form a straight angle.
Important: discuss why the second solution would not work if DE was only nearly parallel to AC, but not exactly parallel. (Can a proof be made if the line DE is not parallel to AC? Here the angle DBA will be a little more/less than s and the angle EBC will be the same amount less/more than w. But then it is clear that it is easier to have DE parallel to AC.)
-
Ensure that all the students fully understand each of these solutions. Discuss the elegance of the first solution, and the historical significance of the second solution. It is similar to the one used by the famous mathematician, Euclid.
-
Because the mathematics discussed in this session is of major significance it is worth getting the students to make a poster (or something similar) that indicates why the angles in a triangle make a straight angle.
Session 3
In this session the students will use the arrow to investigate angles in polygons.
-
Explain the difference between interior and exterior angles (see below).
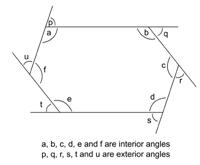
-
Practice drawing and measuring exterior angles for a variety of polygons.
-
Investigation: Use the arrow to investigate the sum of the exterior angles in 3, 4, 5, and 6 sided polygons. Take particular care to watch the arrow turn. In particular it is vitally important to notice as it passes through each half turn. For instance, if the arrow goes through two full turns, the students will need to have watched carefully to notice that the total angle is 720º and not 360º. Get them to carefully write down and justify their results.
-
Does the result hold for all polygons? See if they can find a fault to their results. For example, can they find a funny shaped polygon that is a counter-example to one of their results? If they can’t see it for themselves, get them to check out their results for a polygon that has a concave vertex such as the one shown below.
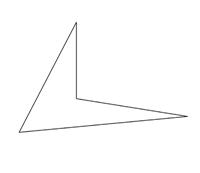
-
Show the students how to triangulate a polygon. That is, show them how to divide the interior of a polygon into triangles by drawing rays from a chosen vertex to every other vertex.
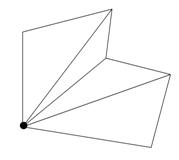
-
Can all polygons be triangulated in this way? Hopefully they will be able to find polygons such as that shown below.
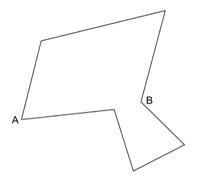
-
Can they show that the above shape cannot be triangulated in the way described starting at A?
Can it be triangulated from some other vertex?
(Try to let them discover that it can be triangulated from B.) -
Problem: Show that any 4-sided polygon can be triangulated into 2 triangles. Find similar results for 5-sided, 6-sided, 7-sided and 8-sided polygons. [These can be triangulated into, respectively, 3, 4, 5 and 6 triangles.]
-
These sorts of investigations sometimes throw up interesting examples. These are to be welcomed as opportunities to think about situations that are in some way unexpected. See below, for example, where A, B and C lie on a straight line, and a triangulation is attempted from C.
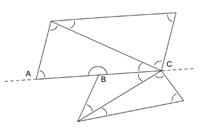
At first sight the interior angles may appear to be the sum of four triangles. But at closer inspection it will be evident that there is a straight angle at B (equivalent to the interior angles of a fifth triangle). Thus the interior angles are equivalent to five sets of 180º. This same example could also be dealt with as below.
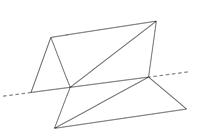
-
Problem: Explain why the sum of the interior angles of a polygon is the same as the sum of the interior angles of the triangles that triangulate it.
-
Problem: Explain why the sum of the interior angles in degrees of an n-sided polygon (n – 2) x 180. [This follows from the previous two results.]
Session 4
In this session the ideas encountered in the previous sessions are consolidated.
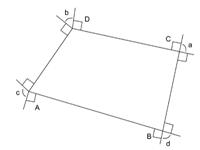
-
The students draw the 4-sided figure ABCD (see above). Then at each vertex lines perpendicular to the joining sides are drawn as shown. Thus angles a, b, c and d are formed.
-
Investigate: Using the arrow, the students are to investigate the angles a, b, c and d. That is, they should try to find some true things (theorems) about these angles and carefully explain why these things are true. [For example, students should be able to show, using the TM, that a + b + c + d = 360º. They could also show, for example, that the angle ADC is 180 – b degrees, because the four angles at the point D make 360º.]
Are their results true for all 4-sided convex polygons? (A convex polygon is one without any concave vertices of the sort found on an arrow head. In other words the interior angle at each vertex is less than 180º.)
If so, how do they know? -
Again, they need to carefully explain and justify their results.
-
Let them investigate 3-sided, 5-sided and 6-sided convex polygons in the same way.
-
Then ask them to investigate polygons with one concave vertex (such as the arrow head) in the same way.
Session 5
In this session the ideas developed in previous sessions are linked with the idea of a locus.
The whole session is based on an open-ended problem. Students should be encouraged to proceed carefully using the sorts of ideas developed in previous sessions. In particular they should be alert for possible counter-examples. And they should state their results carefully, and justify them.
-
Investigation: The students should imagine that they have a polygon and a circle rolling around its outside. See, for instance, below.
-
What is the shape and length of the locus mapped out by the centre of the circle as it rolls completely around the polygon?
This investigation can lead to far more mathematics than can be covered in a single session. So students will be able to work productively on it in a way that is accessible to them. There are some very elegant results to be found. There are also some interesting challenges to be encountered in situations that involve concave vertices (but do not draw any attention to this until the students actually decide to distinguish between convex and concave cases).
For those students who experience difficulty the following suggestions may be useful (depending on the difficulty encountered). You might suggest:
Carefully investigate the situation where the polygon is a square (this is probably the easiest special case, and arguably the best place to begin). [The students should be able to find that the shape is a figure with quarter-circle corners and straight edges. The length is the sum of the perimeters of the initial square and the initial circle.]
Cut out a cardboard square. Cut out a cardboard circle and make a hole in the centre of the circle for your pencil. Carefully roll the circle round the square and let the pencil draw the shape. Give particular attention to the shape of the locus as the circle rolls around each vertex.
Once a square has been successfully solved, move on to a rectangle. Then an equilateral triangle. Gradually build up to harder and harder cases.
Students should find that for all convex polygons the length is the sum of the perimeters of the initial polygon and the circle. However, this result does not hold for polygons with concave vertices such as those in the diagram below. This can be justified through a careful examination of one special case.
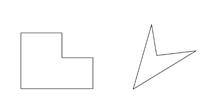
The result for such concave cases is probably beyond the students at this level. However, it is not beyond them to show that the result for convex cases does not hold in these new cases.
There are other situations that the result does not work for, for example, that shown below.

Again, it is enough for the students to realise that these are exceptions to the situation that applies to convex cases.