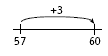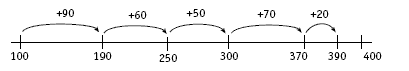All that Glitters

In this activity, students use their knowledge of the basic facts that add up to 10 to make rounded or tidy numbers to work with. They then use their knowledge of place value and addition strategies.
The students need to have the opportunity to explore the situations in these activities on their own and to discuss the answers. You could then discuss and model with them a variety of strategies they could use to solve the problems in the activities.
You could use a variety of modelling materials to make this activity practical. For example:

• $1 coins in toy money (if you have enough);

• sets of place value equipment, such as loose nursery sticks, bundles of 10 nursery sticks, and bags of 10 bundles;

• loose beans (commercially made or from the supermarket), film canisters or small plastic bags of 10 beans, and a box for 10 canisters/bags to show 100 beans;

• Unifix blocks, loose, in sticks of 10, and in boxes of 100.

The students could model 18 pieces of gold and add to the model to get to the nearest tidy number. They could record their answers as 18 + 2 = 20 and make links to their basic facts, for example, 8 + 2 = 10, so 18 + 2 = 20 and 28 + 2 = 30.
More able students may be able to use an empty number line to make their rounded or tidy numbers.

The students could also use a hundreds board (Material Master 4-4) to make their rounded or tidy numbers and to help them add.
In question 2, the students will have the amounts 20, 70, 50, 60, 90, and 100. It is very important that they have place value equipment (as in question 1) available to help them to solve this problem.
There is already one bag of 100 pieces, so you could ask the students to join the remaining bags to the 100-piece bag. Starting with the largest number is a useful strategy for those students whose addition strategy is to count on: 100 + 90 would be 100, 110, 120, 130, 140, 150, 160, 170, 180, 190. As the students count, they should physically move the place value sets of 10 so that they don’t lose track. As they make each new set of 100, they should start another set of 100 so that they
can see their total at a glance.
The students could use a thousands book (Material Master 4-7) to help them to recognise the number sequence beyond 100.
Students with more advanced addition strategies may be able to add together pairs of numbers:
100 + 90 = 190, 60 + 50 = 110, 70 + 20 = 90
so 110 + 90 = 200 and 200 + 190 = 390
Encourage the students to discuss which pairs of numbers they added and why. For example, “I chose 50 + 60 = 110 because I know 50 + 50 = 100, so it’s just 10 more.”
The students may also be able to use a 400-number line, marked in decades, to solve the addition problem.

Question 3 involves grouping the bags so that they do not exceed 150. The students should investigate this on their own and then share their results. If they come up with two bags each day for 3 days, for example, 100 + 50, 90 + 60, and 20 + 70, you could ask if they can find a way to bank three bags on 1 day. Does this reduce the number of days needed to bank the gold?
As an extension, you could ask the students this question:
“The next time Supple-Jack is ashore, he has these bags to bank:

He has no more gold pieces, but he wants to bank all the gold. What can he do?”
This will encourage the students to find compatible numbers that add up to 100. To answer the question, they need to be secure in their knowledge of basic facts and have the ability to add by using part-whole strategies. For example, 23 + 47 = 70 because 20 + 40 = 60 and 3 + 7 = 10, so 60 + 10 = 70.
 

Answers to Activity

1. a. 2
b. 3
c. 1
d. 3
e. 1
f. 2
2. 390
3. 3 days