This is a level 5 algebra strand activity from the Figure It Out series.
A PDF of the student activity is included.
Click on the image to enlarge it. Click again to close. Download PDF (113 KB)
use a table to find a pattern
write a quadratic equations to describe the relationship
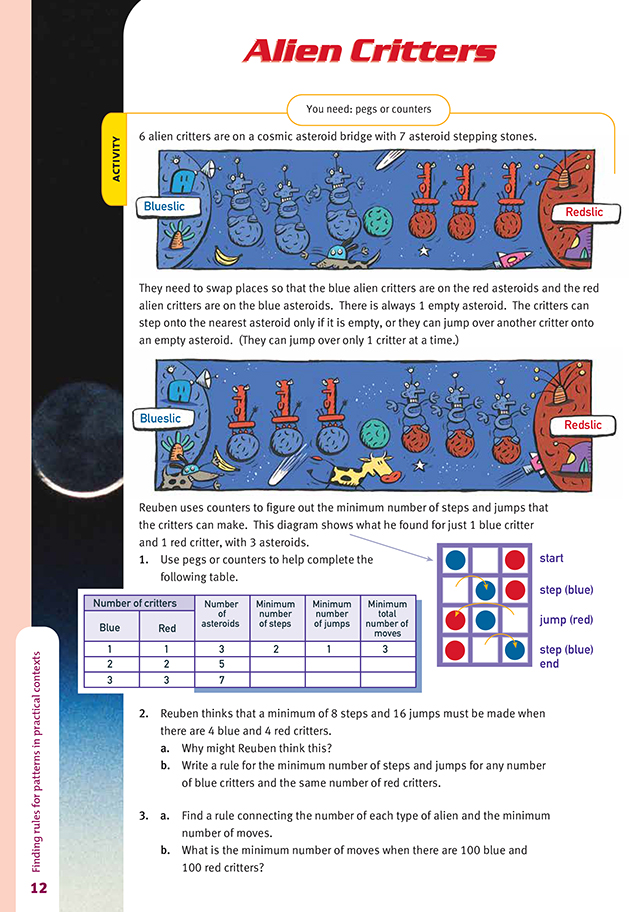
FIO, Level 4+, Algebra, Book Four, Alien Critters, page 12
pegs or counters
In this activity, students must first systematically explore the moves involving steps, S, and jumps, J, for equal numbers of blue and red alien critters to swap positions on an “asteroid bridge”. The bridge always has 1 more asteroid than there are alien critters. So for 3 blue and 3 red alien critters, there are 7 asteroids.
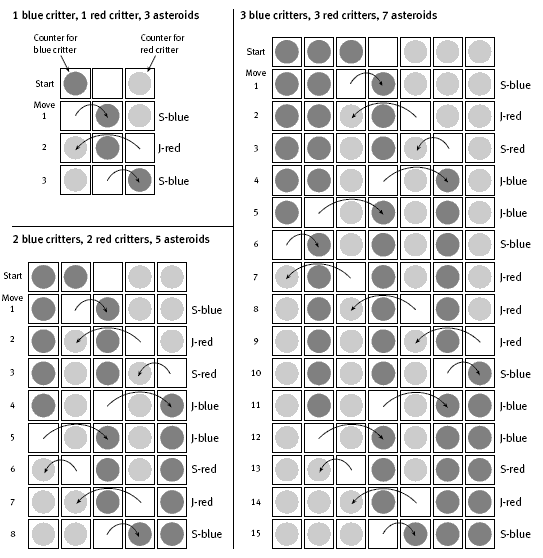
The students will need to use equipment such as pegs on a pegboard or counters on squared paper to actually carry out the moves. They will also need to devise a sensible way to monitor the sequence of moves they make. In the following diagram, S-blue indicates that a step was made by a blue critter, and J-red indicates that a jump was made by a red critter.
Note that, in each table, there is rotational symmetry about the middle of the table. If each table, excluding any labels and arrows, were rotated a half-turn (180 degrees) about its middle, the table would look exactly as it did prior to the half-turn being made. This kind of symmetry can often be shown when such position swapping occurs.
As indicated, the students will need to work carefully to ensure that the number of steps and jumps they make is accurately determined. It is also important that the students accurately assess the minimum number of moves of each type. Combinations of moves that use more than the minimum are also possible, but if the numbers in the table are greater than they ought to be, it is very unlikely that the students will be able to devise rules for the number of steps and jumps. For this reason, it may be helpful to have the students share their results for the minimum number of moves for different numbers of critters.
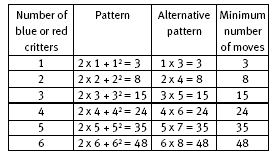
The completed table for question 2 in the Answers shows that “the minimum number of steps is twice the number of blue or red critters” and that “the minimum number of jumps is the square of the number of blue or red critters”. In looking for patterns in the table, the students may come up with alternative rules for the minimum number of steps. For example, “the minimum number of steps is equal to the total number of blue and red critters,” or “the minimum number of steps is equal to 1 less than the number of asteroids”.
They are likely to find the rule for the minimum number of jumps challenging. Encourage them to look for a direct relationship between the number of blue (or red) critters and the minimum number of jumps. Here are these rules shown algebraically:
The table for question 3 in the Answers shows an alternative way to generalise the minimum number of moves for any number of blue or red critters. Here is the rule shown algebraically:
The pattern in the table indicates that the minimum number of moves can be found by multiplying the number of blue (or red) critters by 2 more than the number of blue (or red) critters. So, for example, when there are 23 of each kind of alien critter, the minimum number of moves is 23 x 25 = 575. Note also that
n(n + 2) = n2 + 2n. This shows that the two rules are equivalent. So when n = 23, the least number of moves can be calculated from either 23 x 25 = 575 or 23 x 23 + 2 x 23 = 575. The students may notice other patterns, for example, that the total number of moves is 1 less than the square of (the number of blue (or red) critters plus 1). Algebraically, the number of moves = (n + 1)2 – 1. So, for example, when n = 23, the total number of moves is (23 + 1)2 – 1 = 24 x 24 – 1 = 575.
Once again, it can be shown that the rules (n + 1)2 – 1 and n2 + 2n are equivalent:
(n + 1)2 – 1 = n2 + n + n + 1 – 1
= n2 + 2n + 1 – 1
= n2 + 2n
Answers to Activity
1.
2. a. Reuben may have noticed a pattern in the columns for the minimum number of steps (increase by 2) and the minimum number of jumps (square numbers).
b. A possible rule is: the minimum number of steps is twice the number of blue or red critters. The minimum number of jumps is the square of the number of blue or red critters.
3. a. A possible rule is: the minimum number of moves is the minimum number of steps plus the minimum number of jumps. This can be found using the rules for the number of steps and the number of jumps given for question 2b.
Alternatively, the second pattern in the table below indicates that the minimum number of moves can be found by multiplying the number of red (or blue) critters by 2 more than the number of red (or blue) critters.
b. 2 x 100 + 1002 = 10 200 moves or 100 x (100 + 2) = 10 200 moves.