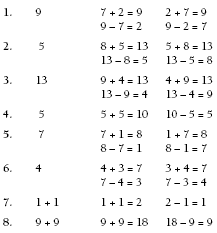This is a level 2 number and algebra strand activity from the Figure It Out series. It relates to Stage 5 of the Number Framework
A PDF of the student activity is included.
Click on the image to enlarge it. Click again to close. Download PDF (208 KB)
know addition facts
write additon facts as equations, e.g 2 + 7 =
Activity One
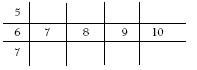
Students may enjoy exploring patterns on a copy of the addition array. For example, the odd and even answers can be shaded with different colours. This produces a diagonal pattern that can be explained by the fact that the answers in each row and column grow consecutively by one. Since odd and even numbers alternate, this produces the odd-even-odd-even shading pattern.
Similarly, students can shade all the spaces with answers of 10, for example, and write the equations:
1 + 9 = 10
2 + 8 = 10
3 + 7 = 10.
They may notice that as one addend increases by one, the other decreases by one.
Subtraction patterns can be investigated by taking an addend (for example, six) and looking across the row to create subtraction equations with that answer.
This creates patterns like this:
7 – 1 = 6
8 – 2 = 6
9 – 3 = 6.
As the number taken from increases by one, the number that is taken must also increase by one to get the same answer. This can be extended with problems such as:
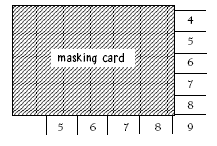
For students who have difficulty reading the array, a rectangular masking card can be useful.
Activity Two
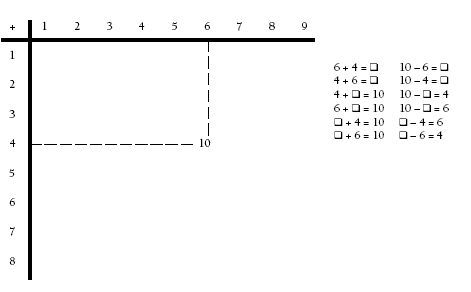
Using an addition array to solve subtraction problems involves the idea of an inverse operation. In this case, subtraction and addition are inverses, that is, one undoes the other. Adding three, for example, can be undone by subtracting three. Any particular triad of numbers in the addition array can be used to solve a variety of problems. For example, consider the triad 4, 6, and 10:
Answers to Activity
Activity One
Note: Each family of facts contains either two or four equations.
Activity Two
1. a. 5
b. 6
c. 7
d. 3
e. 13
f. 12
2. Answers will vary. For a–d, students need to find two of the numbers on the same line. The third number to complete the equation will be on a horizontal or vertical line with the larger of the other two numbers.
For e and f, students need to find the two
numbers in the shaded areas. The largest number will be in the square where they meet.
Each set of three numbers can be used to make and answer a variety of problems.