A4 containers

The Problem

Tipene and his friends have scissors, tape and sheets of A4 paper to construct closed containers from a single sheet of paper.
Tipene's net is a single piece that can be folded or bent to make the container. (He joins the sides with tape not tabs.)
Miri makes a shape where the net is not one piece but can be taped together to make the container (making a more efficient use of paper).
Pepe makes a shape where one face is a square.

Who makes the container with the biggest volume?

Teaching Sequence

1. Begin by giving the students a piece of A4 paper and ask them to make a closed container. At this stage keep the requirements open.
2. Display the containers and discuss:
   Which is the largest?
   What criteria have you used in making your decision?
   Which container has the largest surface area? How do you know?
   Which container has the smallest surface area? How do you know?
   Which container has the largest volume? How do you know?
   Which container has the smallest volume? How do you know?
   Do any of the containers have square faces?
3. Pose the problem to the class.
4. Ask for their initial ideas about which container has the greatest volume. Ask them to explain the thinking behind their guess.
5. Take votes for the containers. List results on the board.
6. Have the students investigate the problem in pairs
7. As the students work ask questions that focus on their understanding of area, volume and perimeter.
   What is the area of this face? How did you work it out?
   What is the volume of your container? How did you work it out?
   What sort of container do you think will have the largest volume? Why?
   How did you start on this problem?
   What understandings are you using to solve this problem?
8. When the students think that they have a solution for the largest container, ask them to make the container from a single sheet of A4.
   Share and discuss containers. Ask:
   Do you think we have found the container with the largest volume? How do we know?

Solution

There is no one solution to this problem. The idea here is to explore shapes and to find ways to measure their volume.

Tipene's net needs to be a single piece that can be folded and taped. The usual net for a cuboid looks something like this:
 
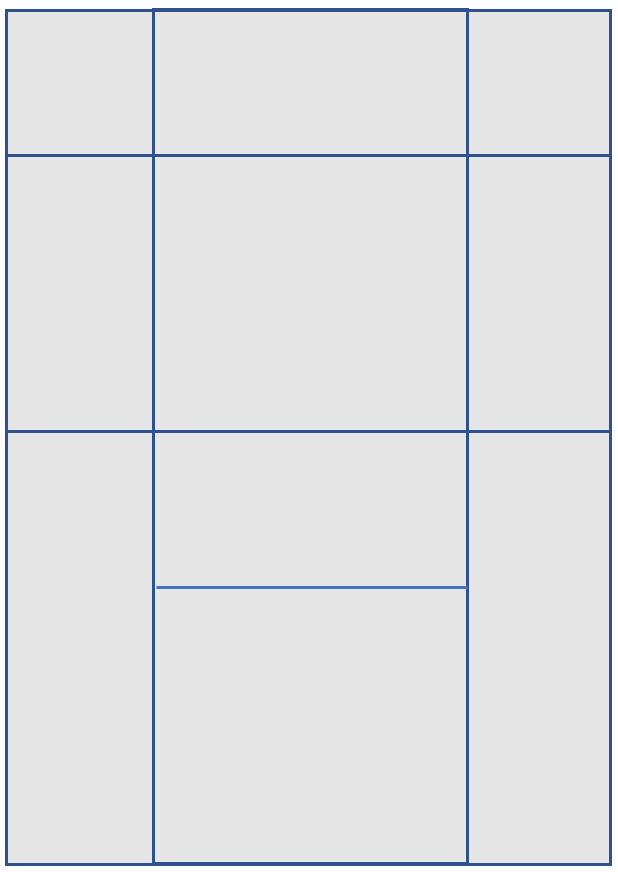
The sides of the pieces can be labelled to make it clear which are equal:

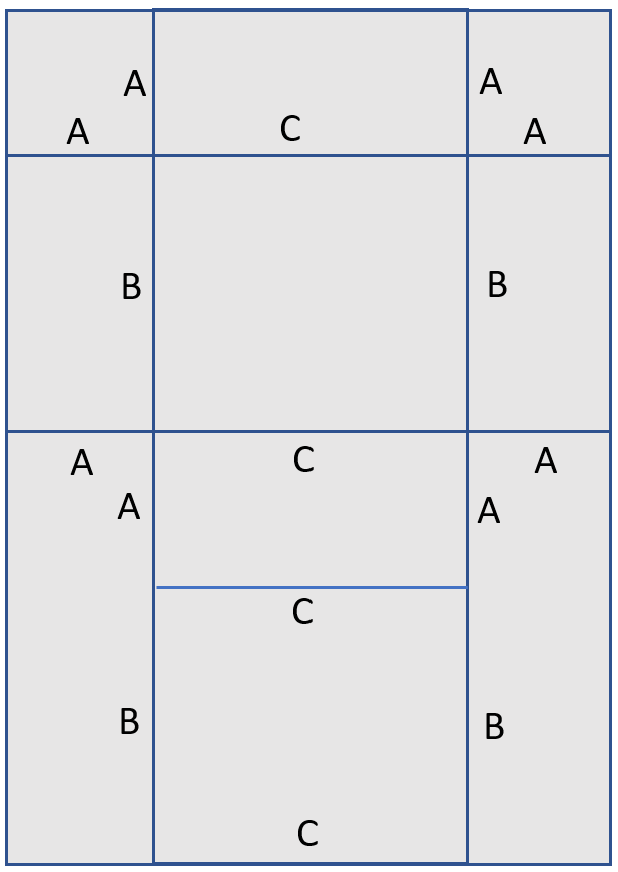
Since an A4 piece of paper is 297mm by 210mm we can now write equations for the length of sides B and C in terms of A:
B = 210 - 2A
C = (297 - 2A) / 2

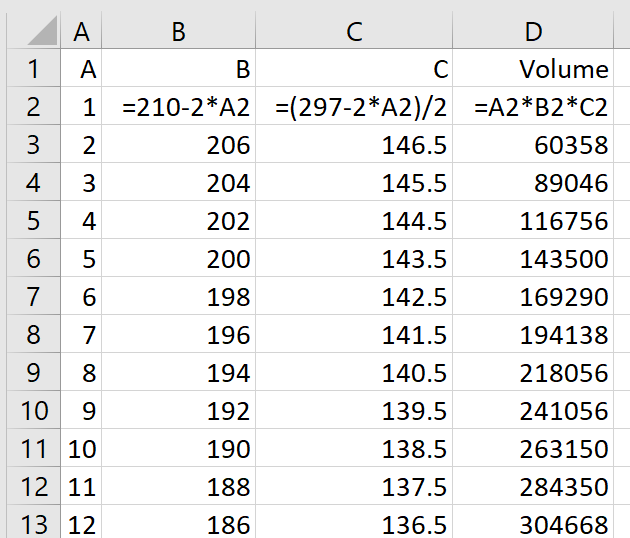
At level 6 students may be able to write an equation for the volume and then find its maximum by taking a derivative and identifying a root. At this level students should be able to create a spreadsheet with a column for A B and C, and a fourth column multiplying those together to find the volume. By filling this spreadsheet down they can identify that the volume is greatest when the length of side A is 40mm.

Because Miri can cut and reattach pieces to make her shape she does not need to have any waste paper. The biggest box she could make would be a cube with the same surface area as the original piece of paper, though this may not be practicable, since it may require cutting the paper into a large number of pieces of various sizes. Regardless, we can calculate the size of this theoretical cube.

The surface area of the original piece of paper is 297mm by 210mm, or 62,370mm².
The surface area of each face of the cube is therefore 62,370mm² ÷ 6, or 10,395mm².
The length of each edge of the cube must be the square root of 10,395mm², which is 102mm (0dp).
The volume of the cube is 102mm x 102mm x 102mm, or 1,061,208mm³, which can be converted to 1061cm³.
(note: if you do not round during calculations, the exact answer is 1059.8cm³ (1dp)).

The problem does not describe how Pepe makes his box other than that at least one side is a square. He may have a solution the same as Miri's, or he may have made a net more like Tipene's.