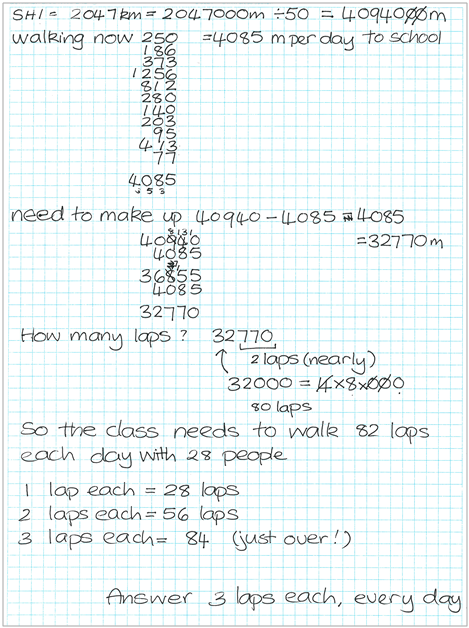The purpose of this activity is to engage students in solving a problem using measurement and arithmetic techniques.
This activity assumes the students have experience in the following areas:
- Converting between metric units of length.
- Multiplying and dividing decimals.
- Adding and subtracting decimals.
- Solving problems with proportions.
The problem is sufficiently open ended to allow the students freedom of choice in their approach. It may be scaffolded with guidance that leads to a solution, and/or the students might be given the opportunity to solve the problem independently.
The example responses at the end of the resource give an indication of the kind of response to expect from students who approach the problem in particular ways.
 A teacher has set her class the task of ‘walking the length’ of State Highway 1 in 50 school days. They are allowed to count each step that each student takes if they walk to and from school and if they walk laps of the 400 m track on the school field at fitness time.
A teacher has set her class the task of ‘walking the length’ of State Highway 1 in 50 school days. They are allowed to count each step that each student takes if they walk to and from school and if they walk laps of the 400 m track on the school field at fitness time.
Use the data the class have collected below, to work out how many laps of the track each student will need to walk on each of the 50 challenge days.
Eleven students walk to school and back home every day. Each walker used a gps app on a smartphone to measure their walk to school. the results are:
250, 186, 373, 1256, 812, 280, 140, 203, 95, 413, 77
The class ‘Googled’ the length of State Highway 1 and got 2 047 km.
The following prompts illustrate how this activity can be structured around the phases of the Mathematics Investigation Cycle.
Make sense
Introduce the problem. Allow students time to read it and discuss in pairs or small groups.
- Do I understand the situation and the words? (Students may need support to understand that the students walk individually around the track to complete the equivalent of the length of SH1.)
- What are the important numbers in the problem? What do the numbers refer to? (The distances students walked are the distance to school, and will need to be doubled to include the distance home. The total of 2047 km and the track distance of 400m are lengths but the problem involves rates, such as distance per student per day.)
- What important ideas are involved? (Sharing the distance among 28 students, sharing the total distance among 50 days. Both require division.)
- Can I represent the problem using a diagram or equations?
Plan approach
Discuss ideas about how to solve the problem. Emphasise that, in the planning phase, you want students to say how they would solve the problem, not to actually solve it.
- How will I know when I have solved the problem? What will my solution look like? (Students need to recognise that they will have a distance for each student to walk each day that can be justified by their working.)
- What strategies can I use to get started? (A diagram or ratio table will be good starting representation.)
- What kinds of calculations will I need to do?
- What tools will be helpful? (Calculators are important for this problem.)
Take action
Allow students time to work through their strategy and find a solution to the problem.
- Have I shown my workings in a way that is easy to follow?
- Does my answer seem correct? Does it seem realistic to the situation? Is the distance per student reasonable?
- How could I make sure that I haven’t missed anything?
- How do my results look different or the same compared to others? Why could this be?
- Is there another possible answer or way to solve it?
Convince yourself and others
Allow students time to check their answers and then either have them pair share with other groups or ask for volunteers to share their solution with the class.
- What is the solution?
- How would I convince someone else I am correct?
- Could I have solved the problem in a more efficient way?
- Which ideas would convince others that my findings answer the investigation question?
- Which ideas or tools worked well in my investigation?
- How could these strategies be used on other problems?
Examples of work
Work sample 1
The student uses appropriate calculations to solve a measurement problem involving proportional reasoning.
Click on the image to enlarge it. Click again to close.
Work sample 2
The student finds the solution to a proportional reasoning problem in a measurement context.