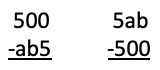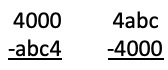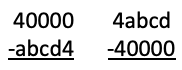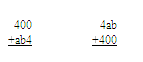This problem solving unit is suitable for Level 5 (or Level 6) students.
- Solve a mathematical problem.
- See how to generalise and extend a problem.
- Understand why and how mathematical statements may be justified.
- Work with others to solve a problem and generate ideas.
Like all of the Problem Solving units, this one aims to introduce students to the underlying ideas of mathematics through a problem. The problem here requires a simple knowledge of arithmetic as well as some knowledge of algebra. However, the process we go through demands a considerable use of ingenuity and creativity. In this unit we see how a mathematical theory might develop through experimentation, conjecturing, proving, generalising and extending. We also see that there is more than one way to justify results and that some of these proofs are ‘nicer’ than others.
As with all of these units it is difficult to break the development here up into lessons, as we can never be quite sure how any particular class will progress. This will depend both on their ability and on your scaffolding. The right question asked at the right time will enable more rapid progress. However, you don’t want to make it too rapid! It is important that they struggle through at least some of the ideas on their own. So you will need to judge when to help them and how much help to give them.
Again like many of the units this one can be used at a variety of Levels. (It also makes a useful workshop for teachers.) Naturally you will expect older students to get further than younger ones. With younger students it is probably enough to solve the 400 problem; be able to do the m00 problem for particular values of m; to see the problem with 4000; and to be able to make some conjectures.
As we have listed this unit for Levels 5 (and 6), we have included some algebra. This may be omitted if you feel that it is too hard for your class. But it does give insight into the usefulness of algebra in its ability to synthesise. Arguing in general here replaces 10 special cases that all follow exactly the same line of reasoning. However, if you do soft pedal the algebra for most of the class, it will be a good extension aspect of the main problem and be invaluable for your brighter students.
- Pencils
- Paper
Lesson Sequence
Session 1
Here we introduce the 400 problem and have a chance to play with the ideas involved.
Background
As usual, first there is a problem
The 400 Problem: Below are two subtraction problems. Both produce the same answer.
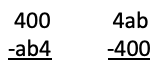
Find a and b.
This can be done in at least three ways.
Method 1. Trial and error: If you use this approach, then it is wise to be systematic. Put a = 0 and try b = 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. Then try a = 1 followed by all the possibilities for b. Then try a = 3 and so on. This is the way a computer would do the problem and would come up with the answer quite quickly. However, it would take a human quite a while so it is not a recommended method unless you cut down the trial in some way.
First it is worth noting that the second sum must have a positive (or zero) answer. This means that a cannot be bigger than 3.
Second, if a = 0, the first answer must be over 300, while the second is less than 10.
Third, if a = 1, the first answer is over 200 while the second answer is less than 100.
Fourth if a = 2, then the first answer is over 100 but the second answer is less than 100.
We know immediately that a = 3. So we know have to find b so that the answers to the two subtractions below are equal.
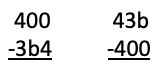
There are various ways to continue from here but they all lead to b = 6.
Method 2. The subtraction algorithm: (We realise that you may use a different subtraction algorithm to the one that we have used here. Whatever you use will work and will give the same answer. In this method work with the first subtraction first. 4 from 0 won’t go. So make the 0 a 10 and change the 40 to 39.
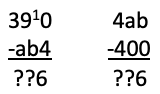
We then have 6 as the last digit of the answer. But then we have to have the same last digit in the answer to the second subtraction. But 0 from b is b. So b = 6.
Rewriting the subtraction sums gives
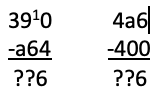
But on the left, 6 from 9 is 3, so now we have
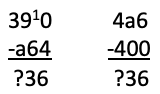
Now 0 from a equals 3 so a = 3. Again we get a = 3 and b = 6.
Method 3. Algebra: We now rewrite the expressions using algebraic. The first sum can be written as
400 – (a x 100 + b x 10 + 4).
The second sum can be written as
400 + a x 10 + b – 400.
But these two expressions are equal so
400 – (a x 100 + b x 10 + 4) = 400 + a x 10 + b – 400.
So
396 – a x 100 – b x 10 = a x 10 + b.
So
396 = a x 100 + a x 10 + b x 10 + b
= a x 110 + b x 11.
Dividing both sides by 11 we get
36 = a x 10 + b.
Since 36 = 3 x 10 + 6, a = 3 and b = 6.
This is a nice little problem but it doesn’t take long to solve – not for the brighter students anyway. So see what happens if we change all the 4s to 5s. We’re then looking at the 500 problem.
The 500 Problem: Below are two subtraction problems. Both the answers they produce are the same.
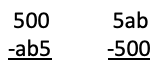
Find a and b.
The same methods that we have already used each give a = 4 and b = 5.
Clearly now we can make up a 300 problem, a 900 problem and so on. To circumvent all this let’s try the m00 problem.
The m00 Problem: Below are two subtraction problems. Both the answers they produce are the same. The letter m stands for any digit.
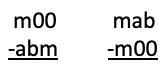
Find a and b.
We’ll talk about tackling the m00 problem in Session 2.
Teaching sequence
- Talk about the problem so that it is understood by all students. Two things may help here.
- It shouldn’t be a problem for Level 5 and 6 students but a and b just stand for digits. So they can be 0, 1, 2, 3, 4, 5, 6, 7, 8, or 9. Further, they stand for the same digit in each subtraction problem. This means that if a is 5 in the first subtraction sum, then it is 5 in the second.
- It might be worth putting a = 2 and b = 8, for example, and doing the two subtractions to see what you get. Clearly the answers will not be the same so the a and b that we want are not 2 and 8. However, it might help the students to get the idea of the problem.
Underline the idea that we are now looking for a and b so that the two answers in the subtraction sums are the same.
- Let them go away in their groups and see if they can find a and b. Some will be able to do this very quickly. There are two responses to this.
- Ask them to write down their working.
- Ask them what question can they think of that is like the 400 problem. Get them to change the 4s in the problem to 5s (or whatever number they come up with) so that they now try the following problem where again they have to find a and b and the two answers are both the same.
They will probably appreciate being asked the second of these more than the first.
- When a reasonable number of the groups have found the values of a and b, bring the whole class together to discuss the ways that the original problem was solved. This will give the slower students a chance to see how the others were thinking. It has been our experience that once many of these students see what the others have done, they will be able to go on and have success in the next part of the question.
- Let the students go back into their groups to try different values instead of 4 in the original problem. You might get each group to do three cases. It might be a good thing to leave some possible values of m out. So, for instance, don’t ask anyone to do m = 7 or m = 9.
- Bring the groups back together. Let them report on what they found. At this point allow the results to be scattered over the board. Don’t look for patterns unless the students insist on doing so.
- Give each group a chance to record what results were obtained and how they obtained them.
Session 2
Here we look at and solve the m00 problem.
Background
Returning to the m00 problem, the following table summarizes what has happened so far.
m a b 1 0 9 2 1 8 3 2 7 4 3 6 5 4 5 6 5 4 7 6 3 8 7 2 9 8 1 There are many patterns here. We list the ones that occur to us.
- a is always one less than m (a = m – 1);
- b is always 10 – m;
- a + b is always 9;
- if we think of ab as being a two-digit number, then ab = 9m.
Your students may well come up with several others. For instance, m = a + 1, which is the same as (i).
How can we prove these? You may well have proved them without knowing.
Method 1: Proof by Exhaustion (check every case): The table shows that for every value of m, each of the four patterns above holds. So the patterns must hold.
So we have a theorem. (It might be worth adding four extra columns to the table headed m – 1, 10 – m, a + b and 9m. When these are filled in , it is easy to see that all four patterns hold.
Theorem: In the m00 problem, each of the four patterns above holds for m = 1, 2, 3, 4, 5, 6, 7, 8, and 9.
Proof: Check each of the 9 values for m.
Method 2: Algebra. If you use the same algebra that we used in Method 3 of the Background to Session 1, we will get some of the patterns (i) to (iv). All we have to do is to replace the 4 in that Method by m. We do this below with the m case under the 4 case.
Proof of (iv): The first sum can be written as
400 – (a x 100 + b x 10 + 4).
[m00 – (a x 100 + b x 10 + m).]
The second sum can be written as
400 + a x 10 + b – 400.
[m00 + a x 10 + b – m00.]
But these two expressions are equal so
400 – (a x 100 + b x 10 + 4) = 400 + a x 10 + b – 400.
[m00 – (a x 100 + b x 10 + m) = m00 + a x 10 + b – m00.]
So
396 – a x 100 – b x 10 = a x 10 + b.
[m00 – m – a x 100 – b x 10 = a x 10 + b.]
So
396 = a x 100 + a x 10 + b x 10 + b = a x 110 + b x 11.
[m00 - m = a x 100 + a x 10 + b x 10 + b = a x 110 + b x 11.
We need one extra step here. m00 – m = m (100 – 1) = m x 99. So
m x 99 = a x 110 + b x 11]
Dividing both sides by 11 we get
36 = a x 10 + b.
[m x 9 = a x 10 + b.]
Since 36 = 3 x 10 + 6, a = 3 and b = 6.
[The last square bracket expression establishes pattern (iv).]
This method shows the power of algebra. By doing pretty well exactly the same work that we did for the 400 problem we have solved the x00 problem. In one move we have settled 9 cases. This seems to be a fairly efficient way to do things.
But this still leaves (i), (ii) and (iii) to be proved.
Proof of (iii): Now we know that m x 9 = a x 10 + b, so m x 9 = a x 9 + a + b. So
a + b = 9(m – a).
This shows that a + b is a multiple of 9. If you add all one-digit numbers together the highest value you get is 18. So a + b must be 9 or 18. But to get 18 we have to have a = 9 = b. But this means that m x 9 = 9 x 10 + 9. Simplifying we see that we have to have m = 11. But m is always less than or equal to 9. So a and b can never both be 9. Hence a + b = 9.
Proof of (i): We now know that a + b = 9, so b = 9 – a. Since m x 9 = a x 10 + b, then m x 9 = a x 10 + (9 – a) = a x 9 + 9. Dividing by 9 we get m = a + 1 or a = m – 1.
Proof of (ii): Since a = 9 – b and m x 9 = a x 10 + b we have m x 9 = (9 – b) x 10 + b. This simplifies to m x 9 = 90 – b x 9. Dividing by 9 gives us the answer we want.
You’ll note here that although the algebraic method is efficient for pattern (iv), it starts to get a little longwinded. The Method of Proof by Exhaustion is by far the quickest here in that it quickly settles all four patterns just by looking down the table.
Teaching Sequence
The first thing to do in this lesson is to recall the results of session 1 and try to find any patterns that exist. You could send them to their groups to think about what patterns they can find. Ask them what might be good way to organize their results (a table such as the one below or some other systematic way is best). Get them to complete the table and write the down patterns the patterns that they find so that someone else can read them out. Tell them that there may be more than one pattern.
x a b 1 2 3 4 5 6 7 8 9
- Get the groups to report back by giving a piece of paper with the pattern on to another group to read out. Make sure that each pattern holds for all of the values of m that you have worked out so far.
- What does each pattern predict for m = 7 and m = 9? Get two volunteers to work out the two missing cases. Make sure that the other students check their work. Do 7 and 9 fit the predicted patterns?
- How can we be sure that these patterns work? This may be done most quickly by the Proof by Exhaustion method. To do this, add extra columns to the table headed m – 1, 10 – m, a + b and m x 9. You might want to push your better students into trying the algebra method. It will be handy in a later Session.
- Give the class time to write up what they have done in this lesson.
- You might ask the better students to consider what might happen if m is bigger than 9.
Session 3
The emphasis in this session turns to finding extensions of the 400 problem. This allows the students to try out their own ideas. It also gives them a chance to see that some problems don’t have answers!
Background
The m00 problem is a generalisation of the 400 problem because with m = 4, the 400 problem is a special case of the m00 problem. An extension of a problem is one that is somehow like the original. We have suggested a few below.Possible Extensions:
- change the subtraction sums to addition sums;
- change the number of zeros in the problem;
- interchange the two numbers in one of the sums or in each of the sums.
Taking up the second of these we have:
The 4000 Problem: Below are two subtraction problems. Both produce the same answer.
Find a, b and c.
You have all the methods that you need to solve this one. We suggest that Method 2 from the Background of Session 1 is the most efficient.
This one is a little tricky. There are no answers. There are no values of a, b and c that will work in this problem. If you use Method 2 as suggested, c wants to be 6, b wants to be 3, and a wants to be 6. But if a is 6, then the first sum has a negative answer. The second sum clearly has a positive answer. So this problem doesn’t work.
It is also true that there are no answers for the corresponding m000 problem.
It might be interesting to see how the algebraic method works. The first sum can be written as
4000 – (a x 1000 + b x 100 + c x 10 + 4).
The second sum can be written as
4000 + a x 100 + b x 10 + c – 4000.
But these two expressions are equal so
4000 – (a x 1000 + b x 100 + c x 10 + 4) = 4000 + a x 100 + b x 10 + c – 4000.
So
3996 – a x 1000 – b x 100 – c x 10 = a x 100 + b x 10 + c.
So
3996 = a x 1000 + a x 100 + b x 100 + b x 10 + c x 10 + c
= a x 1100 + b x 110 + c x 11
= 11(a x 100 + b x 10 + c).The problem now is that 11 is a factor of the right hand side but it is not a factor of the left hand side (11 doesn’t divide exactly into 3996). This means that there are no integers a, b and c that satisfy the last equation. So there are no solutions of the original problem.
If you are trying it for the m000 problem, you’ll end up with m000 – m on the left hand side which is m(1000 – 1) = 999m. Since 11 doesn’t go into 999 (or m), then there are no solutions.
Teaching Sequence
- This lesson is about generalisations and extensions of the 400 problem. Recall the 400 problem and how that led to the m00 problem. Tell them that the m00 problem is a generalisation of the 400 problem because with m = 4, the 400 problem is a special case of the m00 problem. Remind them that an extension of a problem is one that is somehow like the original. Discuss what possible extensions there might be of the 400 problem. (Steer them away from problems with more than four digits.)
- Send them away in their groups to write down three extensions of the 400 problem. Let them choose one of these to solve, write down their solution, and possibly present to the class. Tell them that some of these problems may not give nice or easy answers. Make sure that at least one group attempts the 4000 problem. Try to discourage any group from attempting the 40000 problem.
- After a suitable time, choose a few groups to present their findings. Make sure that one group presents the 4000 problem.
- Discuss what they have done. Let them know that not all problems have answers.
- Give them time to write down their favourite two extensions of the 400 problem along with their solution of one of these.
Session 4
Now we increase the number of zeros to consider the m0000 problem. This has answers and links nicely with the m00 problem.
Background
The 40000 Problem: Below are two subtraction problems. Both the answers they produce are the same.
Find a, b, c and d.
Using any of the previous methods, we find that a = 3, b = 6, c = 3 and d = 6.
It should now be possible to do the m0000 problem for m any digit. The obvious extensions of (i), (ii), (iii), and (iv) apply. The proofs follow exactly as in the m00 problem.
Teaching Sequence
- Refresh the students’ memory of the unit so far. Discuss what generalisations and extensions there could be with no limit on the numbers or on the number of zeros.
- Get them to concentrate on the 40000 problem. Let them tackle this in their groups.
- Encourage them to try the m0000 problem. What results do they get? How are these results related to the m00 problem? What theorem do they get?
- Let the students report back on the results they have found. Talk them through a proof of the theorem. (This can be done using the Method of Exhaustion.)
- Ask the students to write a statement and proof of the theorem.
Session 5
Finally we get to the big overall result that has the original 400 problem as a special case and has been the motivation of this unit. On completing this session they should begin to see how mathematical areas are developed.
Background
The big result here is that if we have m with an even number of zeros we get a solution. The unknowns a, b, c, d, … are, in consecutive pairs, the same as we got in the m00 case. In other words ab = 9m, cd = 9m, … On the other hand if we have an odd number of zeros we get no solutions at all.This is the big generalisation of the original 400 problem. Once we have this result, we can find the answer to the 400 problem by putting m = 4 and the number of zeros equal to 2.
The interesting thing on the proof side is that to prove this for a particular number of zeros all we have to do is to use the algebraic method. Just parallel Method 2 in the Background to Session 2 or the method in the Background to Session 3. Surprisingly, to prove it for an arbitrary number of zeros all at once can be done in the same way but needs just a little care. The problem is keeping track of the zeros associated with each unknown a, b, c, … We don’t give it here as it is a bit complicated.
However, the key to it is that the right hand side is always divisible by 11, whereas the left hand side is m times 99…9 with either an even number of 9s or an odd number of 9s. The former is divisible by 11 and so we can get values for a, b, c, … The latter is not divisible by 11 and so we cannot get values for a, b, c, …
Teaching Sequence
- From the last Session it seems that there might be one final over-arching result here. Discuss what this might be. Produce a conjecture.
- Let the students work in their groups to test the conjecture for various values of m and a different number of zeros.
- Discuss how the conjecture might be proved.
- Let students write a formal statement of the conjecture and attempt a proof.
- Give the students the original problem. Can they all do it easily now?
- Discuss the process that the class has been through with this unit. Talk about the way things have developed from the 400 problem, the proofs that have been used and the generalisations and extensions that have been made.
This week we have been looking at the 400 problem and its extensions. Your student will be able to tell you about it. Together try the problem below.
Below are two addition problems. Both the answers they produce are the same.
Find a and b.
Can you think of some extensions of this problem?